题目内容
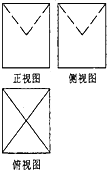 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据几何体的三视图,得出该几何体一个正方体,去掉一个正四棱锥所得的组合体,从而求出该几何体的体积.
解答:
解:根据几何体的三视图,得;
该几何体是一个正方体,去掉一个正四棱锥所得的组合体;
∵正方体的体积为V正方体=1×1×1=1,
正四棱锥的体积为V正四棱锥=
×1×1×
=
;
∴该几何体的体积为V=V正方体-V正四棱锥=1-
=
.
故选:D.
该几何体是一个正方体,去掉一个正四棱锥所得的组合体;
∵正方体的体积为V正方体=1×1×1=1,
正四棱锥的体积为V正四棱锥=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴该几何体的体积为V=V正方体-V正四棱锥=1-
| 1 |
| 6 |
| 5 |
| 6 |
故选:D.
点评:本题考查了空间几何体的三视图的应用问题,也考查了求空间几何体的体积的应用问题,是基础题目.

练习册系列答案
相关题目
函数y=
的图象大致是( )
| 1 |
| x-sinx |
A、 |
B、 |
C、 |
D、 |
若双曲线
-
=1(a>0)的离心率为2,则a等于( )
| y2 |
| a2 |
| x2 |
| 3 |
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
设函数f(x)=x2-12x+20,g(x)=f(x)+|f(x)|,则g(1)+g(2)+…+g(10)=( )
| A、0 | B、9 | C、12 | D、18 |
 某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,
某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,