题目内容
设函数f（x）=x2-12x+20，g（x）=f（x）+|f（x）|，则g（1）+g（2）+…+g（10）=（ ）
| A、0 | B、9 | C、12 | D、18 |
考点：函数的值
专题：函数的性质及应用
分析：解不等式f（x）≥0，从而将g（x）进行化简，然后求和即可．
解答：
解：由f（x）=x2-12x+20≥0得x≥10或x≤2．
所以|f（x）|=
，
所以当x≤2时，g（x）=f（x）+|f（x）|=f（x）+f（x）=2f（x）．
当2＜x≤10时，g（x）=f（x）+|f（x）|=f（x）-f（x）=0．
所以g（1）+g（2）+…+g（10）=g（1）+g（2）=2f（1）+2f（2）=2[1-12+20+4-24+20]=18．
故选D．
所以|f（x）|=
|
所以当x≤2时，g（x）=f（x）+|f（x）|=f（x）+f（x）=2f（x）．
当2＜x≤10时，g（x）=f（x）+|f（x）|=f（x）-f（x）=0．
所以g（1）+g（2）+…+g（10）=g（1）+g（2）=2f（1）+2f（2）=2[1-12+20+4-24+20]=18．
故选D．
点评：本题主要考查一元二次不等式的应用，利用条件去掉绝对值是解决本题的关键，综合性较强．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
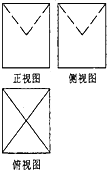某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，其中正视图、侧视图中的两条虚线互相垂直，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，A，B，C是三内角，当sinC（cosAcosB+sinAsinB）-
cos（A+B）取得最大值时，则A=（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的一条渐近线与直线x+3y+1=0垂直，则双曲线的离心率等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
