题目内容
已知f(x)是定义在R上的奇函数,且f(x-2)=f(x+2),当0<x<2时,f(x)=1-log2(x+1),则当0<x<4时,不等式(x-2)f(x)>0的解集是 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的奇偶性结合函数的单调性,得到不等式组,解出即可.
解答:
解:∵f(x-2)=f(x+2),
∴f(x)=f(x+4),函数f(x)是以4为周期的函数,
∵0<x<2时,f(x)=1-log2(x+1),
∴-2<x<0时,f(x)=
-1,
∴2<x<4时,f(x)=
-1,
当0<x<2时,有
,解得:1<x<2,
当2<x<4时,有
,解得:2<x<3,
故答案为:(1,2)∪(2,3).
∴f(x)=f(x+4),函数f(x)是以4为周期的函数,
∵0<x<2时,f(x)=1-log2(x+1),
∴-2<x<0时,f(x)=
| log | (1-x) 2 |
∴2<x<4时,f(x)=
| log | 5-x 2 |
当0<x<2时,有
|
当2<x<4时,有
|
故答案为:(1,2)∪(2,3).
点评:本题考查了函数的单调性和函数的奇偶性,是一道中档题.

练习册系列答案
相关题目
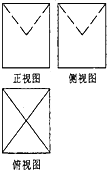 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
如图程序框图中,若输入m=4,n=10,则输出a,i的值分别是( )


| A、12,4 | B、16,5 |
| C、20,5 | D、24,6 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线与直线x+3y+1=0垂直,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线2x-4y+9=0关于点A(2,2)对称的直线方程为( )
| A、2x-4y-1=0 |
| B、2x+4y-1=0 |
| C、2x+4y+1=0 |
| D、4x+2y-1=0 |
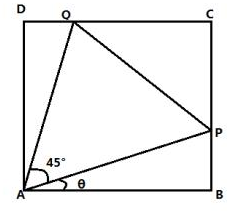 如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.
如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.