题目内容

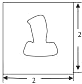某人为估算图中图中不规则图形的面积，将其放置在边长为2的正方形内，然后借助计算机随机向正方形内抛掷1000个点，得知落在不规则图形内的点共有250个，则图中不规则图形的面积约为
 
．
考点：几何概型
专题：概率与统计
分析：先利用古典概型的概率公式求概率，再求不规则图形M的面积的估计值．
解答： 解：由题意，设不规则图形的面积为S，
∵借助计算机随机向正方形内抛掷1000个点，得知落在不规则图形内的点共有250个，
∴概率P=
250
1000
=
1
4
，
∵边长为2的正方形ABCD的面积为4，
∴
S
4
=
1
4
，
∴S=1，
∴不规则图形M的面积的估计值为1．
故答案为：1．
点评：利用几何概型的意义进行模拟试验，估算不规则图形面积的大小，关键是要根据几何概型的计算公式，探究不规则图形面积与已知的规则图形的面积之间的关系，及它们与模拟试验产生的概率（或频数）之间的关系，并由此列出方程，解方程即可得到答案．
练习册系列答案
相关题目
偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=1-x，则关于x的方程f（x）=log9（x+1）解的个数是
 
个．
已知f（x）在（-1，1）上有定义，f(
1
2
)=1，且满足x，y∈（-1，1）时有f(x)-f(y)=f(
x-y
1-xy
)，数列{xn}满足x1=
1
2
，xn+1=
2xn
1+xn2
．
（1）求f（0）的值，并证明f（x）在（-1，1）上为奇函数；
（2）探索f（xn+1）与f（xn）的关系式，并求f（xn）的表达式；
（3）是否存在自然数m，使得对于任意的n∈N*，
1
f(x1)
+
1
f(x2)
+…+
1
f(xn)
＞
m-8
4
恒成立？若存在，求出m的最大值．
已知函数f（x）=x2-2mx+4n2（m∈R，n∈R）．
（Ⅰ）若m从集合{0，1，2，3}中任取一个元素，n从集合{0，1，2，4}中任取一个元素，求方程f（x）=0有两个不相等实数根的概率；
（Ⅱ）若m从区间[0，4]中任取一个数，n从区间[0，6]中任取一个数，求方程f（x）=0没有实数根的概率．
设有关于x的一元二次方程x2+2ax+b2=0
（1）若a是从0，1，2，3四个数中任意取一个数，b是从0，1，2三个数中任意取一个，求上述方程有实根的概率；
（2）若a∈[0，2]，b∈[0，1]，求上述方程有实根的概率．
不等式x-
2
x+1
≥1的解集为
 
．
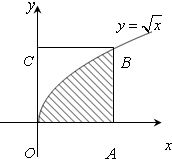在边长为1的正方形OABC中任取一点P，则点P恰好落在正方形与曲线y=
x
围成的区域内（阴影部分）的概率为（　　）
A、
1
2
B、
2
3
C、
3
4
D、
4
5
函数f(x)=lg
x2+1
|x|
（x≠0，x∈R）有如下命题：
（1）函数y=f（x）图象关于y轴对称．
（2）当x＞0时，f（x）是增函数，x＜0时，f（x）是减函数．
（3）函数f（x）的最小值是lg2．
（4）f（x）无最大值，也无最小值．
其中正确命题的序号是
 
．
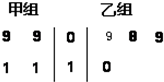如图茎叶图记录了甲、乙两组各四名同学的植树的棵数．
（Ⅰ）从甲、乙两组中各随机取一名学生，求这两名学生植树总棵数为19的概率；
（Ⅱ）甲组中有两名同学约定在早上7点到8点之间到达车站一同去植树，且在车站彼此等候40分钟，超过40分钟，则各自到植树地点再会面．求他们在车站会面的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网