题目内容
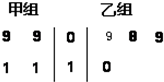 如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.
如图茎叶图记录了甲、乙两组各四名同学的植树的棵数.(Ⅰ)从甲、乙两组中各随机取一名学生,求这两名学生植树总棵数为19的概率;
(Ⅱ)甲组中有两名同学约定在早上7点到8点之间到达车站一同去植树,且在车站彼此等候40分钟,超过40分钟,则各自到植树地点再会面.求他们在车站会面的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(1)分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,而这两名同学的植树总棵数为19的情况有 2+2=4种,由此求得两名同学的植树总棵数为19的概率;
(2)由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|7≤x≤8,7≤y≤8},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|7≤x≤8,7≤y≤8,|x-y|≤
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
(2)由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|7≤x≤8,7≤y≤8},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|7≤x≤8,7≤y≤8,|x-y|≤
| 40 |
| 60 |
解答:
解:(1)由茎叶图可知,甲组同学的植树棵数是:9,9,11,11,
乙组同学的植树棵数是:9,8,9,10.
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,
其中满足这两名同学的植树总棵数为19的情况有 2+2=4种,
这两名同学的植树总棵数为19的概率等于
=
;
(2)由题意知本题是一个几何概型,
试验包含的所有事件是Ω={(x,y)|7≤x≤8,7≤y≤8}
事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|7≤x≤8,7≤y≤8,|x-y|≤
}
事件对应的集合表示的面积是1-2×
=
,
根据几何概型概率公式得到P=
,即他们在车站会面的概率为
.
乙组同学的植树棵数是:9,8,9,10.
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,
其中满足这两名同学的植树总棵数为19的情况有 2+2=4种,
这两名同学的植树总棵数为19的概率等于
| 4 |
| 16 |
| 1 |
| 4 |
(2)由题意知本题是一个几何概型,
试验包含的所有事件是Ω={(x,y)|7≤x≤8,7≤y≤8}
事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|7≤x≤8,7≤y≤8,|x-y|≤
| 40 |
| 60 |
事件对应的集合表示的面积是1-2×
| 1 |
| 9 |
| 7 |
| 9 |
根据几何概型概率公式得到P=
| 7 |
| 9 |
| 7 |
| 9 |
点评:本题主要考查等可能事件的概率,茎叶图的定义以及几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
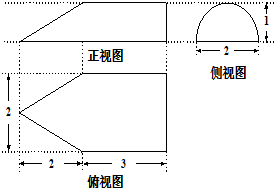
某几何体的三视图(如图),则该几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
点(1,1,1)关于z轴的对称点为( )
| A、(-1,-1,1) |
| B、(1,-1,-1) |
| C、(-1,1,-1) |
| D、(-1,-1,-1) |
若一次函数y=kx+b在(-∞,+∞)上是减函数,则点(k,b)在直角坐标平面的( )
| A、上半平面 | B、下半平面 |
| C、左半平面 | D、右半平面 |
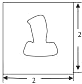 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为