题目内容
函数f(x)=lg
(x≠0,x∈R)有如下命题:
(1)函数y=f(x)图象关于y轴对称.
(2)当x>0时,f(x)是增函数,x<0时,f(x)是减函数.
(3)函数f(x)的最小值是lg2.
(4)f(x)无最大值,也无最小值.
其中正确命题的序号是 .
| x2+1 |
| |x| |
(1)函数y=f(x)图象关于y轴对称.
(2)当x>0时,f(x)是增函数,x<0时,f(x)是减函数.
(3)函数f(x)的最小值是lg2.
(4)f(x)无最大值,也无最小值.
其中正确命题的序号是
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:(1)判断函数是否为偶函数即可.
(2)将复合函数转化为两个基本函数,令t=x+
(x>0),易知在(0,1]上是减函数,在[1,+∞)上是增函数.
(3)由t=x+
≥2(x>0)及偶函数性质可知(3)正确.
(4)由(3)可作出判断.
(2)将复合函数转化为两个基本函数,令t=x+
| 1 |
| x |
(3)由t=x+
| 1 |
| x |
(4)由(3)可作出判断.
解答:
解:(1)函数的定义域为(-∞,0)∪(0,+∞),
又满足f(-x)=f(x),∴函数y=f(x)的图象关于y轴对称,(1)正确.
(2)x>0时,f(x)=lg(x+
),令t=x+
(x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,(2)不正确.
(3)∵t=x+
≥2,又f(x)是偶函数,∴函数f(x)的最小值是lg2,(3)正确.
(4)由(3)知,(4)不正确.
故答案为:(1)(3).
又满足f(-x)=f(x),∴函数y=f(x)的图象关于y轴对称,(1)正确.
(2)x>0时,f(x)=lg(x+
| 1 |
| x |
| 1 |
| x |
(3)∵t=x+
| 1 |
| x |
(4)由(3)知,(4)不正确.
故答案为:(1)(3).
点评:本题通过多个命题来考查函数复合函数的研究方法,涉及了函数的奇偶性,单调性,最值等,知识点,方法灵活,要细心耐心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
若存在 x∈(-∞,0)使得方程2x-
-a=0成立,则实数a的取值范围是( )
| 1 |
| x-1 |
| A、(2,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(0,1) |
某几何体的三视图(如图),则该几何体的体积是( )
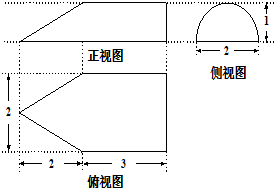

A、
| ||
B、
| ||
C、
| ||
D、
|
点(1,1,1)关于z轴的对称点为( )
| A、(-1,-1,1) |
| B、(1,-1,-1) |
| C、(-1,1,-1) |
| D、(-1,-1,-1) |
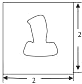 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为