题目内容
已知函数f(x)=x2-2mx+4n2(m∈R,n∈R).
(Ⅰ)若m从集合{0,1,2,3}中任取一个元素,n从集合{0,1,2,4}中任取一个元素,求方程f(x)=0有两个不相等实数根的概率;
(Ⅱ)若m从区间[0,4]中任取一个数,n从区间[0,6]中任取一个数,求方程f(x)=0没有实数根的概率.
(Ⅰ)若m从集合{0,1,2,3}中任取一个元素,n从集合{0,1,2,4}中任取一个元素,求方程f(x)=0有两个不相等实数根的概率;
(Ⅱ)若m从区间[0,4]中任取一个数,n从区间[0,6]中任取一个数,求方程f(x)=0没有实数根的概率.
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)为古典概型,只需列举出所有的基本事件和符合条件的基本事件,作比值即可;
(Ⅱ)为几何概型,只要得出两个区域的面积,由几何概型的公式可得.
(Ⅱ)为几何概型,只要得出两个区域的面积,由几何概型的公式可得.
解答:
解:(Ⅰ)∵m取集合{0,1,2,3}中任一个元素,n取集合{0,1,2,4}中任一个元素,
∴基本事件(m,n)共有16个:(0,0),(0,1),(0,2),(0,4),(1,0),(1,1),(1,2),
(1,4),(2,0),(2,1),(2,2),(2,4),(3,0),(3,1),(3,2),(3,4).…(2分)
设“方程f(x)=0有两个不相等的实根”为事件A,
当m≥0,n≥0时,方程f(x)=0有两个不相等实根的充要条件为m>2n
当m>2n时,事件A共有4个:(1,0),(2,0),(3,0),(3,1),…(4分)
∴方程f(x)=0有两个不相等实数根的概率为p(A)=
=
…(6分)
(Ⅱ)∵m从区间[0,4]中任取一个数,n从区间[0,6]中任取一个数,则试验的全部结果构成区域Ω={(m,n)|0≤m≤4,0≤n≤6},
这是一个矩形区域,其面积S=4×6=24…(8分)
设“方程f(x)=0没有实根”为事件B,则事件B所构成的区域为β={(m,n)|0≤m≤4,0≤n≤6,m<2n}它所表示的部分为梯形,
其面积S1=24-
×4×2=20…(10分)
由几何概型的概率计算公式可得方程f(x)=0没有实数根的概率为p(B)=
=
=
…(12分)
∴基本事件(m,n)共有16个:(0,0),(0,1),(0,2),(0,4),(1,0),(1,1),(1,2),
(1,4),(2,0),(2,1),(2,2),(2,4),(3,0),(3,1),(3,2),(3,4).…(2分)
设“方程f(x)=0有两个不相等的实根”为事件A,
当m≥0,n≥0时,方程f(x)=0有两个不相等实根的充要条件为m>2n
当m>2n时,事件A共有4个:(1,0),(2,0),(3,0),(3,1),…(4分)
∴方程f(x)=0有两个不相等实数根的概率为p(A)=
| 4 |
| 16 |
| 1 |
| 4 |
(Ⅱ)∵m从区间[0,4]中任取一个数,n从区间[0,6]中任取一个数,则试验的全部结果构成区域Ω={(m,n)|0≤m≤4,0≤n≤6},
这是一个矩形区域,其面积S=4×6=24…(8分)
设“方程f(x)=0没有实根”为事件B,则事件B所构成的区域为β={(m,n)|0≤m≤4,0≤n≤6,m<2n}它所表示的部分为梯形,
其面积S1=24-
| 1 |
| 2 |
由几何概型的概率计算公式可得方程f(x)=0没有实数根的概率为p(B)=
| S1 |
| S |
| 20 |
| 24 |
| 5 |
| 6 |
点评:本题以一元二次方程的根为载体,考查古典概型和几何概型,确定概率模型是关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
下列函数中,在(0,+∞)上为增函数的是( )
| A、y=(x-1)2 | ||
| B、y=x2 | ||
C、y=(
| ||
D、y=
|
若存在 x∈(-∞,0)使得方程2x-
-a=0成立,则实数a的取值范围是( )
| 1 |
| x-1 |
| A、(2,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(0,1) |
 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).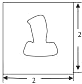 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为