题目内容
|
| A、a<5 |
| B、a≥8 |
| C、2≤a<5 |
| D、5<5或 a≥8 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用平面区域为三角形,建立条件关系即可求m的取值范围.
解答:
解:先作出不等式组
对应的平面区域如图:(阴影部分),
∵不等y≥a表示的平面区域为直线y=a的上.
∴要使不等式组表示的平面区域是一个三角形,
则直线y=a在y=5和y=2之间,
故2≤a<5,
故选:C.
|
∵不等y≥a表示的平面区域为直线y=a的上.
∴要使不等式组表示的平面区域是一个三角形,

则直线y=a在y=5和y=2之间,
故2≤a<5,
故选:C.
点评:本题主要考查线性规划的应用,利用二元一次不等式组和平面区域之间的关系是解决本题的关键,注意利用数形结合.

练习册系列答案
相关题目
在某市举办的城市运动会的跳高比赛中,甲、乙两名跳高运动员一次试跳2米高度成功的概率分别是0.7、0.6,且每次试跳成功与否相互之间没有影响,若甲、乙各试跳两次,则两人中恰有一人第二次才成功的概率为 .
已知命题p:?x∈R,x+2>2x,命题q:?x∈R,x2>0,则( )
| A、命题p∨q是假命题 |
| B、命题p∧(¬q)是真命题 |
| C、命题p∧q是真命题 |
| D、命题p∨(¬q)是假命题 |
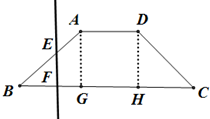 如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2
如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2