题目内容
求证；
（1）sin4α-cos4α=sin2α-cos2α；
（2）sin4α+sin2αcos2α+cos2α=1．
（1）sin4α-cos4α=sin2α-cos2α；
（2）sin4α+sin2αcos2α+cos2α=1．
考点：三角函数恒等式的证明
专题：证明题,三角函数的求值
分析：（1）运用平方差公式和同角的平方关系，即可得证；
（2）运用同角的平方关系，化简即可得证．
（2）运用同角的平方关系，化简即可得证．
解答：
证明：（1）sin4α-cos4α=（sin2α-cos2α）（sin2α+cos2α）
=sin2α-cos2α，
则sin4α-cos4α=sin2α-cos2α；
（2）sin4α+sin2αcos2α+cos2α=sin2α（sin2α+cos2α）+cos2α
=sin2α+cos2α=1，
则sin4α+sin2αcos2α+cos2α=1．
=sin2α-cos2α，
则sin4α-cos4α=sin2α-cos2α；
（2）sin4α+sin2αcos2α+cos2α=sin2α（sin2α+cos2α）+cos2α
=sin2α+cos2α=1，
则sin4α+sin2αcos2α+cos2α=1．
点评：本题考查三角函数的化简和求值、证明，考查同角的平方关系的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
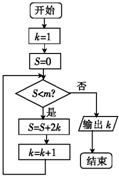执行如图所示的程序框图，若输出的结果是10，则判断框内m的取值范围是（ ）| A、（56，72] |
| B、（72，90] |
| C、（90，110] |
| D、（56，90） |
|
| A、a＜5 |
| B、a≥8 |
| C、2≤a＜5 |
| D、5＜5或 a≥8 |