题目内容
已知哈市南湖f(x)=x2+
-4(x>0),g(x)和f(x)的图象关于原点对称.
(1)求函数g(x)的解析式;
(2)是判断g(x)在(-1,0)上的单调性,并给予证明.
| x |
| 2 |
(1)求函数g(x)的解析式;
(2)是判断g(x)在(-1,0)上的单调性,并给予证明.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的综合应用
分析:(1)可设(x,y)是g(x)图象上的点,所以该点关于原点的对称点(-x,-y)在函数f(x)的图象上,所以便得到-y=x2-
-4,所以便可得到g(x)=-x2+
+4;
(2)求g′(x),根据其在(-1,0)上的符号即可判断g(x)在(-1,0)上的单调性.
| x |
| 2 |
| x |
| 2 |
(2)求g′(x),根据其在(-1,0)上的符号即可判断g(x)在(-1,0)上的单调性.
解答:
解:(1)设(x,y)是g(x)图象上的任意点,根据题意:
点(x,y)关于原点的对称点(-x,-y)在f(x)的图象上;
∴-y=(-x)2-
-4;
∴y=-x2+
+4;
即g(x)=-x2+
+4;
(2)g′(x)=
;
∴x∈(-1,0)时,g′(x)>0;
∴g(x)在(-1,0)上单调递增.
点(x,y)关于原点的对称点(-x,-y)在f(x)的图象上;
∴-y=(-x)2-
| x |
| 2 |
∴y=-x2+
| x |
| 2 |
即g(x)=-x2+
| x |
| 2 |
(2)g′(x)=
| -4x+1 |
| 2 |
∴x∈(-1,0)时,g′(x)>0;
∴g(x)在(-1,0)上单调递增.
点评:考查关于原点对称的两点的坐标表示,在函数图象上的点的坐标满足函数解析式,以及根据函数导数符号判断函数在一区间上的单调性的方法.

练习册系列答案
相关题目
sin(-
)的值是( )
| 13π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
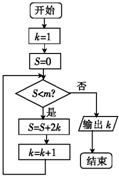 执行如图所示的程序框图,若输出的结果是10,则判断框内m的取值范围是( )
执行如图所示的程序框图,若输出的结果是10,则判断框内m的取值范围是( )| A、(56,72] |
| B、(72,90] |
| C、(90,110] |
| D、(56,90) |
|
| A、a<5 |
| B、a≥8 |
| C、2≤a<5 |
| D、5<5或 a≥8 |
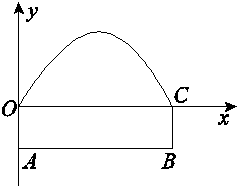 有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?
有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?