题目内容
动点P在直线x+y-1=0上运动，Q（1，1）为定点，当|PQ|最小时，点P的坐标为 ．
考点：两点间距离公式的应用
专题：计算题,直线与圆
分析：线段PQ长的最小值为Q到直线x+y-1=0的距离，PQ：x-y=0，与直线x+y-1=0联立可得P的坐标．
解答：
解：线段PQ长的最小值为Q到直线x+y-1=0的距离，即d=
=
，
此时PQ：x-y=0，
与直线x+y-1=0联立可得P（
，
）．
故答案为：（
，
）．
| 1 | ||
|
| ||
| 2 |
此时PQ：x-y=0，
与直线x+y-1=0联立可得P（
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：（
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查两点间距离公式的应用，考查学生的计算能力，比较基础．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
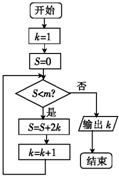执行如图所示的程序框图，若输出的结果是10，则判断框内m的取值范围是（ ）| A、（56，72] |
| B、（72，90] |
| C、（90，110] |
| D、（56，90） |
已知关于x的方程cos2x-sin2x-2sinx+2a+1=0在区间（0，
]内有解，则实数a的取值范围是（ ）
| π |
| 2 |
| A、（-1.1] |
| B、（-1，1） |
| C、[0，1） |
| D、[-1，0） |
|
| A、a＜5 |
| B、a≥8 |
| C、2≤a＜5 |
| D、5＜5或 a≥8 |