题目内容
3.约束条件为$\left\{\begin{array}{l}{x+y-5≤0}\\{x-y-k≤0}\\{x≥0,y≥0}\end{array}\right.$,目标函数Z=2x-y,则Z的最大值是( )| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-5≤0}\\{x-y-1≤0}\\{x≥0,y≥0}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x+y-5=0}\\{x-y-1=0}\end{array}\right.$,解得A(3,2),
化目标函数Z=2x-y为y=2x-Z,由图可知,当直线y=2x-Z过A时,直线在y轴上的截距最小,z有最大值为2×3-2=4.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
11.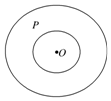 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
18.设p:0<x<5,q:x2-4x-21<0,那么p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.化简 $\overrightarrow{AB}-\overrightarrow{CD}+\overrightarrow{BD}-\overrightarrow{AC}$的结果是( )
| A. | $\overrightarrow 0$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DA}$ |
 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.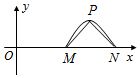 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.