题目内容
12.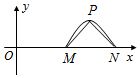 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.
分析 由题意,求出结合函数的图象,图象关于y轴对称,φ=$\frac{π}{2}$,△PMN是以MN为斜边的等腰直角三角形,可得|PM|•sin45°=$\frac{1}{2}$|MN|,且$|MN|•|MP|=2\sqrt{2}$,求解|MN|和A,即得函数f(x)=Asin(ωx+φ)
解答 解:由题意,图象关于y轴对称,φ=$\frac{π}{2}$,
∵△PMN是以MN为斜边的等腰直角三角形,可得|PM|•sin45°=$\frac{1}{2}$|MN|,且$|MN|•|MP|=2\sqrt{2}$,
解得:|MN|=2,|PM|=$\sqrt{2}$
在等腰三角形PMN中,可求的△PMN的高为1,即P点的纵坐标是1,
故得A=1,
T=2|MN|=4,
∴$ω=\frac{2π}{4}=\frac{π}{2}$
∴函数f(x)=Asin(ωx+φ)=sin($\frac{π}{2}x+\frac{π}{2}$)=$cos(\frac{π}{2}x)$,
当x=1时,即f(1)=cos$\frac{π}{2}$=0.
故答案为0.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
2.已知集合A={x|x2-x-2≤0},B=Z,则A∩B=( )
| A. | {-1,0,1,2} | B. | {-2,-1,0,1} | C. | {0,1} | D. | {-1,0} |
3.约束条件为$\left\{\begin{array}{l}{x+y-5≤0}\\{x-y-k≤0}\\{x≥0,y≥0}\end{array}\right.$,目标函数Z=2x-y,则Z的最大值是( )
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
4.在10件同类产品中,有2次品,从中任取3件产品,其中不可能事件为( )
| A. | 3件都是正品 | B. | 至少有1件次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
1.若0<x<1,则$\frac{1}{x}+\frac{2x}{1-x}$的最小值为( )
| A. | $2\sqrt{2}$ | B. | 1+$2\sqrt{2}$ | C. | 2+$2\sqrt{2}$ | D. | 3+$2\sqrt{2}$ |
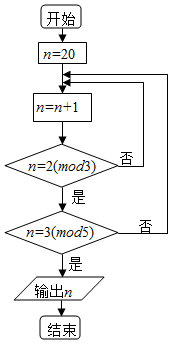 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )