题目内容
11.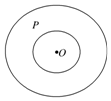 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
分析 点P与点O的距离小于3cm,也就是说以O点为圆心,3CM为半径作一个圆,这个圆的面积减去小圆的面积就是点P与点O的距离小于3cm的机会(一个圆环的面积),而P可能落在的面积为大圆面积减小圆面积,也就是整个圆环的面积,点P与点O距离小于3cm的概率=小圆环的面积:大圆环的面积.
解答  解:如图所示,
解:如图所示,
S大圆环=42π-22π=12π,
S小圆环=32π-22π=5π,
所以,点P与点O距离小于3cm的概率=$\frac{5π}{12π}$=$\frac{5}{12}$.
故选B.
点评 此题考查了几何概率的计算公式,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
相关题目
2.已知集合A={x|x2-x-2≤0},B=Z,则A∩B=( )
| A. | {-1,0,1,2} | B. | {-2,-1,0,1} | C. | {0,1} | D. | {-1,0} |
6.已知函数f(x)=e|x|,函数g(x)=$\left\{\begin{array}{l}{ex,x≤4}\\{4{e}^{5-x},x>4}\end{array}\right.$对任意的x∈[1,m](m>1),都有f(x-2)≤g(x),则m的取值范围是( )
| A. | (1,2+ln2] | B. | (1,$\frac{7}{2}$+ln2] | C. | [ln2,2) | D. | (2,$\frac{7}{2}$+ln2) |
3.约束条件为$\left\{\begin{array}{l}{x+y-5≤0}\\{x-y-k≤0}\\{x≥0,y≥0}\end{array}\right.$,目标函数Z=2x-y,则Z的最大值是( )
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
1.若0<x<1,则$\frac{1}{x}+\frac{2x}{1-x}$的最小值为( )
| A. | $2\sqrt{2}$ | B. | 1+$2\sqrt{2}$ | C. | 2+$2\sqrt{2}$ | D. | 3+$2\sqrt{2}$ |