题目内容
17.“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由圆(x-1)2+(y-m)2=5,令y=0,可得:x-1=$±\sqrt{5-{m}^{2}}$,可得圆(x-1)2+(y-m)2=5被x轴截得的弦长L=$2\sqrt{5-{m}^{2}}$>2,解得m范围即可判断出结论.
解答 解:由圆(x-1)2+(y-m)2=5,令y=0,可得:x-1=$±\sqrt{5-{m}^{2}}$,
∴圆(x-1)2+(y-m)2=5被x轴截得的弦长L=$2\sqrt{5-{m}^{2}}$>2,解得-2<m<2.
∴“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的充分不必要条件.
故选:A.
点评 本题考查了直线与圆相交问题、简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)的图象与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象的对称中心完全相同,则φ=( )
| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
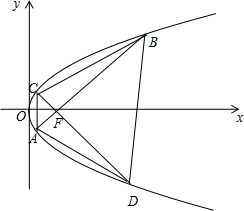 如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.
如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点. 在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.
在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.