题目内容
9.已知函数f(x)=lnx-mx(m为常数),讨论函数f(x)的单调区间.分析 求出函数的定义域,求出f(x)的导数,通过讨论m的范围,求出函数的单调区间即可.
解答 解:f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$-m=-$\frac{m(x-\frac{1}{m})}{x}$,
m>0时,令f′(x)>0,解得:x<$\frac{1}{m}$,
∴当x∈(0,$\frac{1}{m}$)时,f′(x)>0,当x∈($\frac{1}{m}$,+∞)时,f′(x)<0,
∴函数f(x)的单调增区间是(0,$\frac{1}{m}$),单调递减区间是($\frac{1}{m}$,+∞);
m≤0时,f′(x)>0,
∴f(x)在(0,+∞)递增.
点评 本题考查了函数的单调性问题,考查导数的应用,分类讨论思想,是一道中档题.

练习册系列答案
相关题目
17.“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.函数f(x)=cos2x+$\sqrt{3}$sinxcosx,
命题p:?x0∈R,f(x0)=-1,
命题q:?x∈R,f(2π+x)=f(x),
则下列命题中为假命题的是( )
命题p:?x0∈R,f(x0)=-1,
命题q:?x∈R,f(2π+x)=f(x),
则下列命题中为假命题的是( )
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | ¬p∨¬q |
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
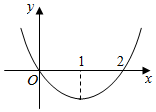

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |