题目内容
12. 在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.
在如图所示的五面体中,四边形ABCD是矩形,平面ADF⊥平面ABEF,且AB∥EF,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,M是EF的中点,N在AM上.(I)求证:DN∥平面BCE;
(Ⅱ)求证:平面ABEF⊥平面ABCD.
分析 (I)通过证明四边形ABEM是平行四边形得出AM∥BE,又AD∥BC,故平面ADM∥平面BCE,所以DN∥平面BCE;
(II)利用勾股定理的逆定理证明AM⊥AF,利用面面垂直的性质得出AM⊥平面ADE,于是AD⊥AM,又AD⊥AB,得出AD⊥平面ABEF,故而面ABEF⊥平面ABCD.
解答 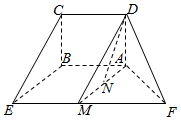 证明(I)连结DM.
证明(I)连结DM.
∵AB∥EF,AB=$\frac{1}{2}$EF,M是EF的中点,
∴AB$\stackrel{∥}{=}$EM,
∴四边形ABEM是平行四边形,
∴AM∥BE,又AM?平面BCE,BE?平面BCE,
∴AM∥平面BCE.
∵四边形ABCD是矩形,
∴AD∥BC,又BC?平面BCE,AD?平面BCE,
∴AD∥平面BCE,
又AD?平面ADM,AM?平面ADM,AD∩AM=A,
∴平面ADM∥平面BCE,
又DN?平面ADM,
∴DN∥平面BCE.
(II)由(I)知AM=BE=2,
∵AF=BE=2,MF=$\frac{1}{2}$EF=2$\sqrt{2}$,
∴AM2+AF2=MF2,∴AM⊥AF.
∵平面ADF⊥平面ABEF,平面ADF∩平面ABEF=AF,AM?平面ABEF,
∴AM⊥平面DAF,∵DA?平面DAF,
∴AM⊥DA,
又∵四边形ABCD是矩形,∴AD⊥AB,
∵AB?平面ABEF,AM?平面ABEF,AB∩AM=A,
∴AD⊥平面ABEF,又AD?平面ABCD,
∴平面ABEF⊥平面ABCD.
点评 本题考查了线面平行的判定,面面垂直的性质与判定.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(4-x),x<4}\\{1+{2}^{x-1},x≥4}\end{array}\right.$,则f(0)+f(log232)=( )
| A. | 19 | B. | 17 | C. | 15 | D. | 13 |
17.“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.在一个二面角的两个面内都和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二面角的余弦值为( )
| A. | $\frac{\sqrt{15}}{6}$ | B. | -$\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | 以上都不对 |