题目内容

6．设直线l1：（a+1）x+3y+2=0，直线l2：x+2y+1=0，若l1∥l2，则a=$\frac{1}{2}$，若l1⊥l2，则a=-7．

分析 直线l1：（a+1）x+3y+2=0，直线l2：x+2y+1=0，分别化为：y=-$\frac{a+1}{3}$x-$\frac{2}{3}$，y=-$\frac{1}{2}$x-$\frac{1}{2}$．利用两条直线平行与垂直的充要条件即可得出．

解答 解：直线l1：（a+1）x+3y+2=0，直线l2：x+2y+1=0，分别化为：y=-$\frac{a+1}{3}$x-$\frac{2}{3}$，y=-$\frac{1}{2}$x-$\frac{1}{2}$．
若l1∥l2，则-$\frac{a+1}{3}$=-$\frac{1}{2}$，解得a=$\frac{1}{2}$．
若l1⊥l2，则$-\frac{a+1}{3}$×$（-\frac{1}{2}）$=-1，解得a=-7．
故答案分别为：$\frac{1}{2}$；-7．

点评 本题考查了两条直线平行与垂直的充要条件、斜截式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
16．数列{an}中，2Sn=n2+n．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=2an•an，求数列{bn}的前n项和Tn．
17．“-1＜m＜1”是“圆（x-1）2+（y-m）2=5被x轴截得的弦长大于2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
14．函数f（x）=cos2x+$\sqrt{3}$sinxcosx，
命题p：?x0∈R，f（x0）=-1，
命题q：?x∈R，f（2π+x）=f（x），
则下列命题中为假命题的是（　　）
A．p∨qB．p∧qC．￢p∧qD．￢p∨￢q
1．大学生村官王善良落实政府“精准扶贫”，帮助贫困户张三用9万元购进一部节能环保汽车，用于出租，假设第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该车每年的运营收入均为11万元，若该车使用了n（n∈N*）年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则n等于3．
11．已知i为虚数单位，复数z=-$\frac{1}{3}$+$\frac{2\sqrt{2}}{3}$i的共轭复数为$\overline{z}$，则$\overline{z}$的虚部为（　　）
A．$\frac{2\sqrt{2}}{3}$B．-$\frac{2\sqrt{2}}{3}$C．$\frac{2\sqrt{2}}{3}$iD．-$\frac{2\sqrt{2}}{3}$i
18．若函数f（x）的导函数f′（x）的图象如图所示．则（　　）
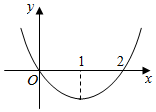
A．x=1是最小值点B．x=0是极小值点
C．x=2是极小值点D．函数f（x）在（1，2）上单调递增
15．定义集合A={x|2x≥1}}，B={x|${{{log}_{\frac{1}{2}}}$x＜0}，则A∩∁RB=（　　）
A．（1，+∞）B．[0，1]C．[0，1）D．[0，2）
16．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，-4），|$\overrightarrow{c}$|=$\sqrt{10}$，且$\overrightarrow{b}$•$\overrightarrow{c}$=$5\sqrt{2}$，则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为（　　）
A．$\frac{2π}{3}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网