题目内容
8.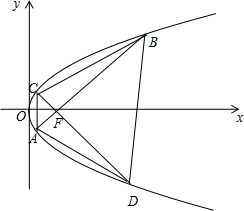 如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.
如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.(1)求抛物线C的方程;
(2)求四边形ACBD面积的最小值.
分析 (1)利用抛物线的定义直接求抛物线C的方程;
(2)过焦点F作两条相互垂直的直线,设AB:x=my+$\sqrt{5}$-1,CD:x=-$\frac{1}{m}$y+$\sqrt{5}$-1(m≠0),联立直线与抛物线方程组成方程组,利用弦长公式,求出|AB|,|CD|,推出四边形ACBD的面积的表达式,利用基本不等式求四边形ACBD面积的最小值.
解答 解:(1)∵直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,
∴(1-$\frac{p}{2}$)2+(2-0)2=5,
∴p=4,
∴抛物线C的方程为y2=8x;
(2)由(1)知:F(2,0)
设AB:x=my+2,CD:x=-$\frac{1}{m}$y+2(m≠0)
由AB方程与抛物线的方程得:y2-8my-16=0
∴|AB|=8(1+m2)
同理:|CD|=8(1+$\frac{1}{{m}^{2}}$).
∴四边形ACBD的面积:S=$\frac{1}{2}|AB||CD|$=32(1+m2)(1+$\frac{1}{{m}^{2}}$)=32(2+m2+$\frac{1}{{m}^{2}}$)≥128.
(当且仅当m2=$\frac{1}{{m}^{2}}$即:m=±1时等号成立)
∴四边形ACBD的面积的最小值为128.
点评 本题考查抛物线的标准方程的求法,直线与抛物线的位置关系的应用,四边形面积的最值以及基本不等式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(4-x),x<4}\\{1+{2}^{x-1},x≥4}\end{array}\right.$,则f(0)+f(log232)=( )
| A. | 19 | B. | 17 | C. | 15 | D. | 13 |
17.“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
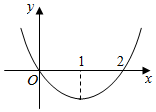

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |