题目内容
7.设定义在R上的函数f(x)满足:f(tanx)=$\frac{1}{cos2x}$,则f(${\frac{1}{2016}}$)+f(${\frac{1}{2015}}$)+…+f(${\frac{1}{2}}$)+f(0)+f(2)+…+f(2015)+f(2016)=1.
分析 由已知中f(tanx)=$\frac{1}{cos2x}$,根据万能公式,可得f(x)的解析式,进而可得f(x)+f( $\frac{1}{x}$)=0,进而可得答案.
解答 解:∵f(tanx)=$\frac{1}{cos2x}$=$\frac{1+ta{n}^{2}x}{1-ta{n}^{2}x}$,
∴f(x)=$\frac{1+{x}^{2}}{1-{x}^{2}}$,f($\frac{1}{x}$)=$\frac{1+(\frac{1}{x})^{2}}{1-(\frac{1}{x})^{2}}$=$\frac{1+{x}^{2}}{{x}^{2}-1}$=-$\frac{1+{x}^{2}}{1-{x}^{2}}$,
∴f(x)+f($\frac{1}{x}$)=0
∴f(${\frac{1}{2016}}$)+f(${\frac{1}{2015}}$)+…+f(${\frac{1}{2}}$)+f(0)+f(2)+…+f(2015)+f(2016)=f(0)=1.
故答案为:1.
点评 本题考查的知识点是三角函数的恒等变换及化简求值,其中根据已知求出f(x)的解析式,以及f(x)+f( $\frac{1}{x}$)=0是解答的关键.

练习册系列答案
相关题目
17.“-1<m<1”是“圆(x-1)2+(y-m)2=5被x轴截得的弦长大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
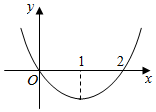

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |
15.定义集合A={x|2x≥1}},B={x|${{{log}_{\frac{1}{2}}}$x<0},则A∩∁RB=( )
| A. | (1,+∞) | B. | [0,1] | C. | [0,1) | D. | [0,2) |
2.在一个二面角的两个面内都和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二面角的余弦值为( )
| A. | $\frac{\sqrt{15}}{6}$ | B. | -$\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | 以上都不对 |
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,-4),|$\overrightarrow{c}$|=$\sqrt{10}$,且$\overrightarrow{b}$•$\overrightarrow{c}$=$5\sqrt{2}$,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |