题目内容
在边长为1的正方形ABCD内任取一点P,则P到点A和C的距离都小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据已知条件,求出满足条件的正方形ABCD的面积,及动点P到定点A的距离|PA|<1对应平面区域的面积,代入几何概型计算公式,即可求出答案.
解答:
解:满足条件的正方形ABCD,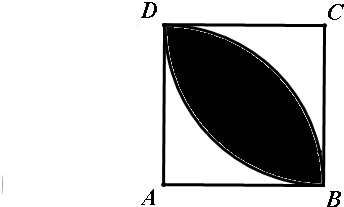
其中满足动点P到点A和C的距离都小于1的平面区域如图中阴影所示:
则正方形的面积S正方形=1
阴影部分的面积S阴影=2(
-
)
故动点P到定点A的距离|PA|<1的概率P=
=
=
;
故选D.

其中满足动点P到点A和C的距离都小于1的平面区域如图中阴影所示:
则正方形的面积S正方形=1
阴影部分的面积S阴影=2(
| π |
| 4 |
| 1 |
| 2 |
故动点P到定点A的距离|PA|<1的概率P=
| S阴影 |
| S正方形 |
| ||
| 1 |
| π-2 |
| 2 |
故选D.
点评:本题考查的知识点是几何概型,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式解答.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
直线x+y+
=0截圆x2+y2=4所得劣弧所对圆心角为( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,asinAsinB+bcos2A=2
a,则
=( )
| 3 |
| b |
| a |
A、2
| ||
B、2
| ||
C、
| ||
D、
|