题目内容
5.已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的图象一段如图,则f(2016)等于( )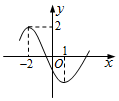
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,从而求得f(2016)的值,
解答 解:根据函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的图象,可得A=2,
$\frac{1}{2}•\frac{2π}{ω}$=1-(-2)=3,∴ω=$\frac{π}{3}$,再结合五点法作图可得-2•$\frac{π}{3}$+φ=$\frac{π}{2}$,∴φ=$\frac{7π}{6}$,
∴f(x)=2sin($\frac{π}{3}$•x+$\frac{7π}{6}$),f(2016)=2sin($\frac{2016π}{3}$+$\frac{7π}{6}$)=2sin(672π+$\frac{7π}{6}$)=2sin$\frac{7π}{6}$=-2sin$\frac{π}{6}$=-1,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,求三角函数的值,属于基础题.

练习册系列答案
相关题目
13.命题“任意x∈R,|x|+x2≥0”的否定是( )
| A. | 任意x∈R,|x|+x2<0 | B. | 存在x∈R,|x|+x2≤0 | ||
| C. | 存在x0∈R,|x0|+x02<0 | D. | 存在x0∈R,|x0|+x02≥0 |
20.集合A={y|y=x-2},B={y|y=$\sqrt{x}$},则x∈A是x∈B的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
14.函数y=log(x-2)(5-x)的定义域是( )
| A. | (3,4) | B. | (2,5) | C. | (2,3)∪(3,5) | D. | (-∞,2)∪(5,+∞) |
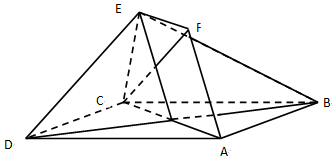 (文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.