题目内容
10.已知等比数列{an}的前n项和为Sn,且S6=S3+14,a6=10-a4,a4>a3.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}中,bn=log2 an,求数列{an•bn }的前n项和Tn.
分析 (1)根据递推公式,即可求数列{an}的通项公式;
(II)求得数列{bn}的通项,再利用错位相减法,即可求得数列{bn}的前n项的和Tn
解答 解:(Ⅰ)由已知a4+a5+a6=14,∴a5=4,
又数列{an}成等比,设公比q,则$\frac{4}{q}$+4q=10,
∴q=2或$\frac{1}{2}$(与a4>a3矛盾,舍弃),
∴q=2,an=4×2n-5=2n-3;
(Ⅱ)bn=n-3,∴an•bn=(n-3)×2n-3,
Tn=-2×2-2-1×2-1+0+…+(n-3)×2n-3,
2Tn=-2×2-1-1×20+0+…+(n-3)×2n-2,
相减得Tn=2×2-2-(2-1+20+…+2n-3)+(n-3)×2n-2=$\frac{1}{2}$-(2n-2-$\frac{1}{2}$)+(n-3)×2n-2
=(n-4)×2n-2+1,
点评 本题考查数列的通项与求和,解题的关键是掌握数列求通项的方法,正确运用错位相减法,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
5.已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的图象一段如图,则f(2016)等于( )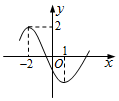
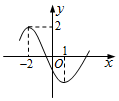
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
2.已知等比数列{an}的公比q=2,其前4项和S4=60,则a3等于( )
| A. | 16 | B. | 8 | C. | -16 | D. | -8 |
20.已知函数f(x)=$\frac{2x}{{{x^2}+1}}$,则下列说法正确的是( )
| A. | 函数f(x)在(0,+∞)上有最小值 | B. | 函数f(x)在(0,+∞)上没有最大值 | ||
| C. | 函数f(x)在R上没有极小值 | D. | 函数f(x)在R上有极大值 |
 已知全集U=R,集合A={x|1≤x≤3},B={x|2<x<4}.
已知全集U=R,集合A={x|1≤x≤3},B={x|2<x<4}.