题目内容
15.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F2,左准线是l,若该双曲线右支上存在点P,使PF2等于P到直线l的距离,则该双曲线离心率的取值范围是(1,$\sqrt{2}+1]$.分析 设P点的横坐标为x,根据该双曲线右支上存在点P,使PF2等于P到直线l的距离,利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.
解答 解:设P点的横坐标为x
∵该双曲线右支上存在点P,使PF2等于P到直线l的距离,
∴根据双曲线的第二定义,可得ex-a=x+$\frac{{a}^{2}}{c}$,
∴(e-1)x=a+$\frac{{a}^{2}}{c}$,
∵x≥a,∴a+$\frac{{a}^{2}}{c}$≥a(e-1)
∴e2-2e-1≤0,
∵e>1,∴∴e∈(1,$\sqrt{2}+1]$.
故答案为(1,$\sqrt{2}+1]$.
点评 本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
5.直线l:x+$\sqrt{3}$y-4=0与圆C:x2+y2=4的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交不过圆心 | D. | 相交且过圆心 |
7.已知△ABC中,AB=$\sqrt{3}$,AC=1,∠CAB=30°,则△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{4}$ |
4.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )
| A. | 60里 | B. | 48里 | C. | 36里 | D. | 24里 |
5.已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的图象一段如图,则f(2016)等于( )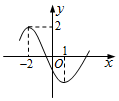
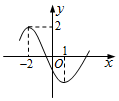
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |