题目内容
15．在四边形 ABCD 中，若$\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{CD}$，则此四边形是（ ）| A． | 平行四边形 | B． | 菱形 | C． | 梯形 | D． | 矩形 |
分析 利用向量共线定理、梯形的定义即可判断出结论．
解答 解：∵$\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{CD}$，
∴AB∥CD，AB≠CD．
∴该四边形为梯形．
答案：C．
点评 本题考查了向量共线定理、梯形的定义，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．已知函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜π）的图象一段如图，则f（2016）等于（ ）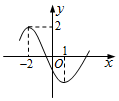
| A． | -1 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
10．已知x，y都是正数，且$\frac{2}{x}+\frac{1}{y}$=1，则x+y的最小值等于（ ）
| A． | 6 | B． | $4\sqrt{2}$ | C． | $3+2\sqrt{2}$ | D． | $4+2\sqrt{2}$ |
20．已知函数f（x）=$\frac{2x}{{{x^2}+1}}$，则下列说法正确的是（ ）
| A． | 函数f（x）在（0，+∞）上有最小值 | B． | 函数f（x）在（0，+∞）上没有最大值 | ||
| C． | 函数f（x）在R上没有极小值 | D． | 函数f（x）在R上有极大值 |