题目内容
9.若幂函数f(x)的图象过点$({\;2\;,\;\frac{{\sqrt{2}}}{2}\;})$,则f-1(2)=$\frac{1}{4}$.分析 由题意知f(2)=2α=$\frac{\sqrt{2}}{2}$,从而可得f(x)=${x}^{-\frac{1}{2}}$,f-1(x)=$\frac{1}{{x}^{2}}$,从而解得.
解答 解:∵幂函数f(x)的图象过点$({\;2\;,\;\frac{{\sqrt{2}}}{2}\;})$,
∴f(2)=2α=$\frac{\sqrt{2}}{2}$,
解得,α=-$\frac{1}{2}$,
故f(x)=${x}^{-\frac{1}{2}}$,
∴f-1(x)=$\frac{1}{{x}^{2}}$,
∴f-1(2)=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$;
故答案为:$\frac{1}{4}$.
点评 本题考查了幂函数的应用及反函数的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19.设不等式x2-x≤0的解集为M,则M为( )
| A. | [0,1) | B. | (0,1) | C. | [0,1] | D. | (-1,0] |
17.直线ax+by=0与圆x2+y2+ax+by=0的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
4.复数z=$\frac{a-i}{1+i}$(a∈R,i是虚数单位)在复平面上对应的点不可能位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.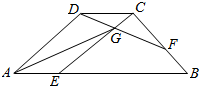 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )| A. | $\frac{11}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{14}{33}$ | D. | $\frac{35}{56}$ |
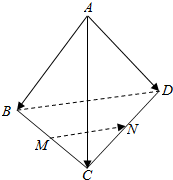 已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.
已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.