题目内容
18．
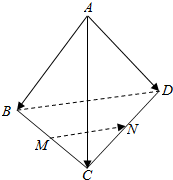已知空间四边形ABCD，连接AC、BD，设M，N分别是BC，CD的中点，则$\overrightarrow{MN}$用$\overrightarrow{AB}$，$\overrightarrow{AC}$，$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$．
分析 根据中位线的性质及向量数乘、向量减法的几何意义，便可得出$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$．
解答 解：$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{BD}=\frac{1}{2}（\overrightarrow{AD}-\overrightarrow{AB}）$=$\frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$．
故答案为：$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$．
点评 考查中位线的性质，以及向量减法和数乘的几何意义，向量数乘的运算．
练习册系列答案
相关题目
8．过抛物线y2=4x的焦点F的直线交抛物线于A，B两点，点O是原点，若|AF|=4，则△AOF的面积为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{4\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |