题目内容
4.复数z=$\frac{a-i}{1+i}$(a∈R,i是虚数单位)在复平面上对应的点不可能位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数代数形式的乘除运算化简,由实部和虚部不同时大于0说明z在复平面上对应的点不可能位于第一象限.
解答 解:∵$z=\frac{a-i}{1+i}$=$\frac{(a-i)(1-i)}{(1+i)(1-i)}=\frac{a-1-(a+1)i}{2}=\frac{a-1}{2}-\frac{a+1}{2}i$,
∴z在复平面上对应的点的坐标为($\frac{a-1}{2},-\frac{a+1}{2}$),
若a-1>0,则a>1,∴a+1<0.
∴z在复平面上对应的点不可能位于第一象限.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
14.在△ABC中,若a2=b2+c2-$\sqrt{3}$bc,则角A的度数为( )
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
16.一个几何体的三视图如图所示,则这个几何体的体积等于( )
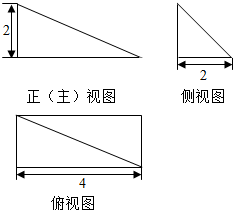

| A. | 12 | B. | 4 | C. | $\frac{16}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
14.函数y=2sin(2x+$\frac{π}{3}$)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
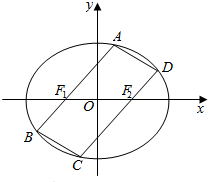 已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.