题目内容
1.设$\overrightarrow{x}$=$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{y}$=$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{z}$=$\overrightarrow{c}$+$\overrightarrow{a}$,且{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,给出下列向量组:①{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{x}$};②{$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$};③{$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{z}$};④{$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$}.其中可以作为空间的基底的向量组有②③④.分析 只要所给三个向量不共面即可作为空间向量的基底.
解答 解:∵$\overrightarrow{x}$=$\overrightarrow{a}$+$\overrightarrow{b}$,∴$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{x}$共面,∴①{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{x}$}不能作为空间向量的一个基底.
∵$\overrightarrow{x}$=$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{y}$=$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{z}$=$\overrightarrow{c}$+$\overrightarrow{a}$,∴$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$不共面,∴②{$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{z}$}可作为空间向量的一个基底.
同理,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{z}$不共面,$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$不共面,∴③{$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{z}$};④{$\overrightarrow{x}$,$\overrightarrow{y}$,$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$}都可作为空间向量的一个基底.
故答案为②③④.
点评 本题考查空间向量的基本定理及其意义,解题的关键是熟练掌握空间向量基本定理意义,掌握向量组可作为基底的条件.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案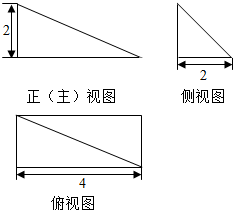
| A. | 12 | B. | 4 | C. | $\frac{16}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
| A. | e1e2=1 | B. | e1e2=2 | C. | e1+e2=2 | D. | $\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$=2 |
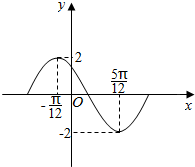 函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.
函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.