题目内容
已知一条曲线C在y轴右边,C上每一点到点F(
,0)的距离减去它到y轴距离的差都是
.
(1)求曲线C的方程;
(2)P是曲线C上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求曲线C的方程;
(2)P是曲线C上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(x,y)是曲线C上任意一点,那么点P(x,y)满足:
-x=
,x>0,由此能求出曲线C的方程.
(2)设P(x0,y0),B(0,b),C(0,c),不妨设b>c.直线PB的方程(y0-b)x-x0y+x0b=0.由圆心(1,0)到PB的距离为1,得(x0-2)b2+2y0b-x0=0,同理(x0-2)c2+2y0c-x0=0.由此能求出S△PBC的最小值为8.
(x-
|
| 1 |
| 2 |
(2)设P(x0,y0),B(0,b),C(0,c),不妨设b>c.直线PB的方程(y0-b)x-x0y+x0b=0.由圆心(1,0)到PB的距离为1,得(x0-2)b2+2y0b-x0=0,同理(x0-2)c2+2y0c-x0=0.由此能求出S△PBC的最小值为8.
解答:
 解:(1)设P(x,y)是曲线C上任意一点,
解:(1)设P(x,y)是曲线C上任意一点,
那么点P(x,y)满足:
-x=
,x>0,化简得y2=2x,x>0.
∴曲线C的方程是y2=2x,x>0.…(5分)
(2)设P(x0,y0),B(0,b),C(0,c),不妨设b>c.
直线PB的方程:y-b=
x,
化简得 (y0-b)x-x0y+x0b=0.
又圆心(1,0)到PB的距离为1,
=1,
故(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
由题意知x0>2,上式化简得(x0-2)b2+2y0b-x0=0,
同理有(x0-2)c2+2y0c-x0=0.
∴b+c=
,bc=
,则(b-c)2=
.
∵P(x0,y0)是抛物线上的点,有y02=2x0,
则(b-c)2=
,b-c=
.
∴S△PBC=
(b-c)•x0
=
•x0
=(x0-2)+
+4≥2
+4=8.…(11分)
当(x0-2)2=4时,上式取等号,此时x0=4,y0=±2
.
因此S△PBC的最小值为8. …(13分)
 解:(1)设P(x,y)是曲线C上任意一点,
解:(1)设P(x,y)是曲线C上任意一点,那么点P(x,y)满足:
(x-
|
| 1 |
| 2 |
∴曲线C的方程是y2=2x,x>0.…(5分)
(2)设P(x0,y0),B(0,b),C(0,c),不妨设b>c.
直线PB的方程:y-b=
| y0-b |
| x0 |
化简得 (y0-b)x-x0y+x0b=0.
又圆心(1,0)到PB的距离为1,
| |y0-b+x0b| | ||
|
故(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
由题意知x0>2,上式化简得(x0-2)b2+2y0b-x0=0,
同理有(x0-2)c2+2y0c-x0=0.
∴b+c=
| -2y0 |
| x0-2 |
| -x0 |
| x0-2 |
| 4x02+4y02-8x0 |
| (x0-2)2 |
∵P(x0,y0)是抛物线上的点,有y02=2x0,
则(b-c)2=
| 4x02 |
| (x0-2)2 |
| 2x0 |
| x0-2 |
∴S△PBC=
| 1 |
| 2 |
=
| x0 |
| x0-2 |
=(x0-2)+
| 4 |
| x0-2 |
| 4 |
当(x0-2)2=4时,上式取等号,此时x0=4,y0=±2
| 2 |
因此S△PBC的最小值为8. …(13分)
点评:本题考查曲线方程的求法,考查三角形面积的最小值的求法,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
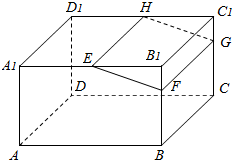 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G