题目内容
在周长为48的直角三角形MPN中，∠MPN=90°，tan∠PMN=
，求以M、N为焦点且过点P的双曲线方程．
| 3 |
| 4 |
考点：双曲线的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：以直线MN为x轴，MN的垂直平分线为y轴，建立直角坐标系，利用周长，即可求出双曲线方程．
解答：
解：建立如图所示的坐标系，设PN=3x，则PM=4x，
∵∠MPN=90°，
∴MN=5x，
∵周长为48，
∴3x+4x+5x=48，
∴x=4，
∴2a=4x-3x=4，2c=5x=20，
∴a=2，c=10，b2=96，
∴以M、N为焦点且过点P的双曲线方程为
-
=1．
解：建立如图所示的坐标系，设PN=3x，则PM=4x，∵∠MPN=90°，
∴MN=5x，
∵周长为48，
∴3x+4x+5x=48，
∴x=4，
∴2a=4x-3x=4，2c=5x=20，
∴a=2，c=10，b2=96，
∴以M、N为焦点且过点P的双曲线方程为
| x2 |
| 4 |
| y2 |
| 96 |
点评：本题考查双曲线的标准方程，考查分析与运算能力即规范的书写表达能力，属于中档题．
练习册系列答案
相关题目
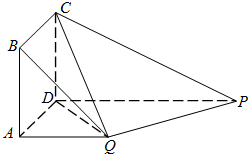在如图所示的多面体中，四边形ABCD为正方形，四边形ADPQ是直角梯形，AD⊥DP，CD⊥平面PDAQ，AB=AQ=
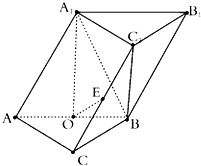三棱柱ABC-A1B1C1，平面A1ABB1⊥平面ABC，AA1=AB=2，∠A1AB=60°，AC=BC=