题目内容
13.已知关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,则$\frac{b}{a}$的取值范围是( )| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
分析 令f(x)=x2+(a+1)x+a+2b+1,由于关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,可得f(0)>0,f(1)<0,再利用线性规划的有关知识即可得出.
解答  解:令f(x)=x2+(a+1)x+a+2b+1,
解:令f(x)=x2+(a+1)x+a+2b+1,
∵关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,
∴f(0)>0,f(1)<0,
∴a+2b+1>0,1+a+1+a+2b+1<0,
即a+2b+1>0,2a+2b+3<0,
设$\frac{b}{a}$=k,即b=ka,
联立$\left\{\begin{array}{l}a+2b+1=0\\ 2a+2b+3=0\end{array}\right.$,解得P(-2,$\frac{1}{2}$).
∴-1<k<-$\frac{1}{4}$,
故选:A
点评 本题考查了二次函数的性质、线性规划的有关知识、一元二次方程有实数根的条件,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
3.复数 Z=$\frac{2-i}{1+i}$的共轭复数对应的点在复平面内位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.下列函数为偶函数的是( )
| A. | y=x-1 | B. | y=$\sqrt{x}$ | C. | y=x2 | D. | y=x3 |
1.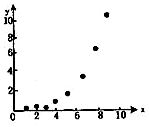 如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )
如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )
 如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )
如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )| A. | $R_1^2>R_2^2$ | B. | $R_1^2<R_2^2$ | C. | $R_1^2=R_2^2$ | D. | 无法确定 |
8.函数f(x)=48x-x3,x∈[-3,5]的最小值为( )
| A. | 128 | B. | -128 | C. | -117 | D. | 115 |
18.在△ABC中,角A,B,C所对的三边分别是a,b,c,已知$A={30°},c=2\sqrt{3},b=2$,则△ABC的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
5.抛物线C:y2=2px(p>0)的焦点与圆F:x2+y2-4x=0的圆心重合,点A,B,C在该抛物线上,且点F是△ABC的重心,则|FA|+|FB|+|FC|的值是( )
| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
3.已知关于x的不等式x2-4ax+3a2<0(a<0)的解集为(x1,x2),则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最大值是( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $-\frac{{4\sqrt{3}}}{3}$ |