题目内容
3.复数 Z=$\frac{2-i}{1+i}$的共轭复数对应的点在复平面内位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:Z=$\frac{2-i}{1+i}$=$\frac{(2-i)(1-i)}{(1+i)(1-i)}$=$\frac{1-3i}{2}$=$\frac{1}{2}-\frac{3}{2}$i的共轭复数$\frac{1}{2}+\frac{3}{2}$i对应的点$(\frac{1}{2},\frac{3}{2})$在复平面内位于第一象限.
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若函数f(x)=lnx+$\frac{a}{x}$在区间[1,e]上最小值为$\frac{3}{2}$,则实数a的值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{e}$ | C. | $\frac{e}{2}$ | D. | 非上述答案 |
8.一个红色的棱长是3cm的正方体,将其适当分割成棱长为1cm的小正方体,则三面涂色的小正方体有( )
| A. | 6个 | B. | 8个 | C. | 16个 | D. | 27个 |
12.下列判断错误的是( )
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
13.已知关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,则$\frac{b}{a}$的取值范围是( )
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
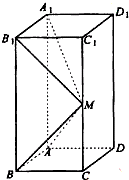 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,