题目内容
4．下列函数为偶函数的是（ ）| A． | y=x-1 | B． | y=$\sqrt{x}$ | C． | y=x2 | D． | y=x3 |
分析 对选项一一判断，可得A，D为奇函数，B为非奇非偶函数，C为偶函数．
解答 解：A，为反比例函数，且为奇函数；
B，定义域为{x|x≥0}不关于原点对称，不为偶函数；
C，为二次函数，关于y轴对称，为偶函数；
D，为三次函数，图象关于原点对称，为奇函数．
故选：C．
点评 本题考查函数的奇偶性的判断，属于基础题．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
12．下列判断错误的是（ ）
| A． | “|am|＜|bm|”是“|a|＜|b|”的充分不必要条件 | |
| B． | 命题“?x∈R，ax+b≤0”的否定是“?x0∈R，ax0+b＞0” | |
| C． | 若￢（p∧q）为真命题，则p，q均为假命题 | |
| D． | 命题“若p，则￢q”为真命题，则“若q，则￢p”也为真命题 |
19．下列函数为偶函数的是（ ）
| A． | y=x+1 | B． | y=x2 | C． | y=x2+x | D． | y=x3 |
9．已知向量$\overrightarrow a=（1，-2）$，$\overrightarrow b=（2，λ）$，且$\overrightarrow a$与$\overrightarrow b$的夹角为锐角，则实数λ的取值范围是（ ）
| A． | （-∞，1） | B． | （-∞，1] | C． | （-∞，-4）∪（-4，1] | D． | （-∞，-4）∪（-4，1） |
16．平行于直线l：2x-y=0且与圆x2+y2=5相切的直线的方程是（ ）
| A． | 2x-y+=0或2x-y-=0 | B． | 2x+y+=0或2x+y-=0 | ||
| C． | 2x-y+5=0或2x-y-5=0 | D． | 2x+y+5=0或2x+y-5=0 |
13．已知关于x的方程x2+（a+1）x+a+2b+1=0的两个实根分别为x1，x2，且0＜x1＜1，x2＞1，则$\frac{b}{a}$的取值范围是（ ）
| A． | $（-1，-\frac{1}{4}）$ | B． | $（-1，-\frac{1}{4}]$ | C． | （-1，+∞） | D． | $（-∞，-\frac{1}{4}）$ |
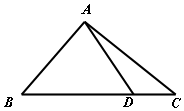如图，已知D是△ABC边BC上一点．