题目内容
8．函数f（x）=48x-x3，x∈[-3，5]的最小值为（ ）| A． | 128 | B． | -128 | C． | -117 | D． | 115 |
分析 由f'（x）=48-3x2=3（16-x2）=3（4-x）（4+x），令f'（x）=0，得x1=-4，x2=4，列表讨论能求出函数f（x）=48x-x3在区间x∈[-3，5]上的最小值．
解答 解：由f'（x）=48-3x2=3（16-x2）=3（4-x）（4+x）
令f'（x）=0即3（4-x）（4+x）=0，∴x1=-4，x2=4
又x∈[-3，5]，列表：
| x | -3 | （-3，4） | 4 | （4，5） | 5 |
| f'（x） | + | 0 | - | ||
| f（x） | -117 | ↗ | 128 | ↘ | -27 |
此函数的递增区间为（-3，4），减区间为（4，5），
当x=4时，此函数的极大值为128，
又f（-3）=-117，f（5）=-27，
∴f（x）的最小值为f（-3）=-117．
故选：C．
点评 本题主要考查了利用函数的导数求出函数的单调性以及函数的极值问题，考查学生分析解决问题的能力，利用导数研究函数的单调性的能力，解题时要认真审题，注意导数性质的合理运用．是中档题．
练习册系列答案
相关题目
18．若函数f（x）=lnx+$\frac{a}{x}$在区间[1，e]上最小值为$\frac{3}{2}$，则实数a的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\sqrt{e}$ | C． | $\frac{e}{2}$ | D． | 非上述答案 |
19．下列函数为偶函数的是（ ）
| A． | y=x+1 | B． | y=x2 | C． | y=x2+x | D． | y=x3 |
16．平行于直线l：2x-y=0且与圆x2+y2=5相切的直线的方程是（ ）
| A． | 2x-y+=0或2x-y-=0 | B． | 2x+y+=0或2x+y-=0 | ||
| C． | 2x-y+5=0或2x-y-5=0 | D． | 2x+y+5=0或2x+y-5=0 |
3．一元二次方程2x2+bx+c=0（a，b∈R）的一个根为1+i，则c=（ ）
| A． | -4 | B． | 0 | C． | 2 | D． | 4 |
13．已知关于x的方程x2+（a+1）x+a+2b+1=0的两个实根分别为x1，x2，且0＜x1＜1，x2＞1，则$\frac{b}{a}$的取值范围是（ ）
| A． | $（-1，-\frac{1}{4}）$ | B． | $（-1，-\frac{1}{4}]$ | C． | （-1，+∞） | D． | $（-∞，-\frac{1}{4}）$ |
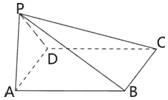如图，平面PAD⊥平面ABCD，ABCD是边长为2的菱形，PA=PD，且∠APD=90°，∠DAB=60°．