题目内容
18.在△ABC中,角A,B,C所对的三边分别是a,b,c,已知$A={30°},c=2\sqrt{3},b=2$,则△ABC的面积为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 根据三角形的面积公式计算即可.
解答 解:∵$A={30°},c=2\sqrt{3},b=2$,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×2×2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
故选:B.
点评 本题考查了求三角形的面积,考查三角形的面积公式,是一道基础题.

练习册系列答案
相关题目
8.一个红色的棱长是3cm的正方体,将其适当分割成棱长为1cm的小正方体,则三面涂色的小正方体有( )
| A. | 6个 | B. | 8个 | C. | 16个 | D. | 27个 |
9.已知向量$\overrightarrow a=(1,-2)$,$\overrightarrow b=(2,λ)$,且$\overrightarrow a$与$\overrightarrow b$的夹角为锐角,则实数λ的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
6.不等式|x|•(1-2x)>0的解集是( )
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
13.已知关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,则$\frac{b}{a}$的取值范围是( )
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
10.如图是一个空间几何体的三视图,则该几何体体积是( )
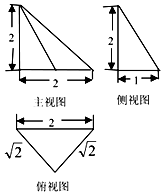

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
8.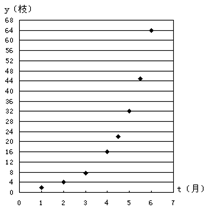 如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
 如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )| A. | 二次函数:y=2t2 | B. | 幂函数:y=t3 | ||
| C. | 指数函数:y=2t | D. | 对数函数:y=log2t |