题目内容
1.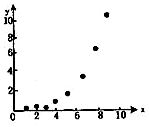 如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )
如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )| A. | $R_1^2>R_2^2$ | B. | $R_1^2<R_2^2$ | C. | $R_1^2=R_2^2$ | D. | 无法确定 |
分析 根据回归模型的相关指数的意义进行判断即可.
解答 解:根据散点图知,利用指数回归模型模拟效果要好于线性回归模型,
所以线性回归模型的相关指数$R_1^2$小于指数回归模型的相关指数$R_2^2$.
即R12<R22.
故选:B.
点评 本题考查了回归模型的相关指数的意义与应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列判断错误的是( )
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
9.已知向量$\overrightarrow a=(1,-2)$,$\overrightarrow b=(2,λ)$,且$\overrightarrow a$与$\overrightarrow b$的夹角为锐角,则实数λ的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
16.平行于直线l:2x-y=0且与圆x2+y2=5相切的直线的方程是( )
| A. | 2x-y+=0或2x-y-=0 | B. | 2x+y+=0或2x+y-=0 | ||
| C. | 2x-y+5=0或2x-y-5=0 | D. | 2x+y+5=0或2x+y-5=0 |
6.不等式|x|•(1-2x)>0的解集是( )
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
13.已知关于x的方程x2+(a+1)x+a+2b+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,则$\frac{b}{a}$的取值范围是( )
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
10.如图是一个空间几何体的三视图,则该几何体体积是( )
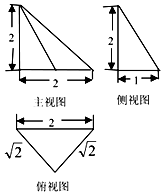

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
11.已知△ABC中,内角A、B、C所对的边分别为a、b、c,若a2=b2+c2-bc,a=3,则△ABC的面积的最大值为( )
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |