题目内容
4．双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是（ ）| A． | y=$±\frac{5}{4}$x | B． | y=$±\frac{4}{5}$x | C． | y=$±\frac{16}{25}$x | D． | y=±$\frac{25}{16}$x |
分析 根据双曲线的方程求得渐近线方程为y=±$\frac{b}{a}$x，即可求出，
解答 解：双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1中a=4，b=5，
故其渐近线方程是y=±$\frac{5}{4}$x，
故选：A．
点评 本题考查双曲线的标准方程，以及双曲线的简单性质的应用，属于基础题．
练习册系列答案
相关题目
14．已知m．n是空间两条不同的直线，α是一个平面，则下列命题为假命题的是（ ）
| A． | m⊥α，n∥α⇒m⊥n | B． | m⊥α，n⊥α⇒m∥n | ||
| C． | m⊥α，n⊥m⇒n∥α或n?α | D． | m∥α，n⊥m⇒n⊥α或n∥α或n?α |
15．函数y=cos2x，x∈R的最小正周期为（ ）
| A． | 2 | B． | π | C． | 2π | D． | $\frac{1}{π}$ |
12．某次考试，班主任从全班同学中随机抽取一个容量为8的样本，他们的数学、物理分数对应如下表：
绘出散点图如下：
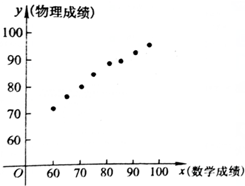
根据以上信息，判断下列结论：
①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高．
其中正确的个数为（ ）
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
根据以上信息，判断下列结论：
①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高．
其中正确的个数为（ ）
| A． | 0 | B． | 3 | C． | 2 | D． | 1 |
19．已知向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（ ）
| A． | （4，-4） | B． | （6，8） | C． | （5，12） | D． | （3，11） |
9．将函数y=sin2x的图象向左平移$\frac{π}{3}$个单位长度，所得图象的函数解析式为（ ）
| A． | y=sin（2x+$\frac{π}{3}$） | B． | y=sin（2x-$\frac{π}{3}$） | C． | y=sin（2x+$\frac{2π}{3}$） | D． | y=sin（2x+$\frac{π}{6}$） |
16．已知函数f（x）=x3-x+3，则曲线y=f（x）在点（1，f（1））处的切线方程为（ ）
| A． | 2x-y+1=0 | B． | x-2y+1=0 | C． | 2x+y+1=0 | D． | 2x-y+2=0 |
13．
已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（ ）
已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 0 |
16．
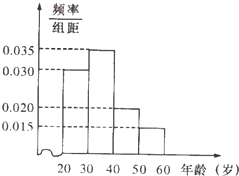某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60）分成四组，其频率分布直方图如图所示．工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表所示．假设两项培训是相互独立的，结业考试也互不影响．
（1）若用分层抽样法从全厂工人中抽取一个容量为40的样本，求四个年龄段应分别抽取的人数；
（2）根据频率分布直方图，估计全厂工人的平均年龄；
（3）随机从年龄段[20，30）和[40，50）中各抽取1人，设这两人中AB两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．
某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60）分成四组，其频率分布直方图如图所示．工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表所示．假设两项培训是相互独立的，结业考试也互不影响．| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 27 | 16 |
| [30，40） | 28 | 18 |
| [40，50） | 26 | 9 |
| [50，60] | 6 | 4 |
（2）根据频率分布直方图，估计全厂工人的平均年龄；
（3）随机从年龄段[20，30）和[40，50）中各抽取1人，设这两人中AB两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．