题目内容
9.将函数y=sin2x的图象向左平移$\frac{π}{3}$个单位长度,所得图象的函数解析式为( )| A. | y=sin(2x+$\frac{π}{3}$) | B. | y=sin(2x-$\frac{π}{3}$) | C. | y=sin(2x+$\frac{2π}{3}$) | D. | y=sin(2x+$\frac{π}{6}$) |
分析 利用左加右减的原则,直接推出平移后的函数解析式即可.
解答 解:将函数y=sin2x的图象向左平移$\frac{π}{3}$个单位后所得到的函数图象对应的解析式为:y=sin[2(x+$\frac{π}{3}$)]=sin(2x+$\frac{2π}{3}$).
故选:C.
点评 本题考查三角函数的图象变换,注意平移变换中x的系数为1,否则容易出错误,属于基础题.

练习册系列答案
相关题目
20.在等差数列{an},若a3=16,a9=80,则a6等于( )
| A. | 13 | B. | 15 | C. | 17 | D. | 48 |
17.设A={1,3,5},B={1,2,3},则A∩B等于( )
| A. | {1,2,3,5} | B. | {1,2,3} | C. | {1,3,5} | D. | {1,3} |
4.双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是( )
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{16}{25}$x | D. | y=±$\frac{25}{16}$x |
14.设m、n、l是空间三条不同的直线,α是一个平面.下列四个命题中为真命题的是( )
| A. | m⊥l,m∥n,则n∥l | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n?α,则m⊥n | D. | 若m∥α,n?α,则m∥n |
1.等比数列{an}的前n项的和分别为Sn,S5=2,S10=6,则a16+a17+a18+a19+a20=( )
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
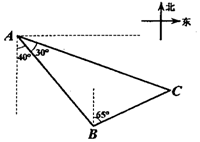 如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.
如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.