题目内容
13. 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 0 |
分析 利用中点,取AD的中点为F,连接EF,CE则EF∥BD,所以异面直线CE与EF所成的夹角就是CE与BD所成的夹角,利用余弦定理求解.
解答 解:设AD的中点为F,连接EF,CE,则EF∥BD,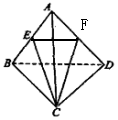
∴异面直线CE与EF所成的夹角就是CE与BD所成的夹角,
由题意:设正四面体ABCD的棱长为2a,则EF=a,CE=CF=$\sqrt{3}$a,
由余弦定理可得cos∠CEF=$\frac{E{F}^{2}+E{C}^{2}-C{F}^{2}}{2×EF×EC}=\frac{\sqrt{3}}{6}$
故选A
点评 本题考查两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
3.执行如图的程序框图,若p=4,则输出的S=( )


| A. | $\frac{7}{8}$ | B. | $\frac{15}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{63}{64}$ |
4.双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是( )
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{16}{25}$x | D. | y=±$\frac{25}{16}$x |
8.i是虚数单位,复数$\frac{5i}{1-2i}$等于( )
| A. | 2-i | B. | 1-2i | C. | -2+i | D. | -1+2i |
4.在三角形ABC中,“sinA>sinB”是“A>B”的( )
| A. | 充分不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 以上都不是 |
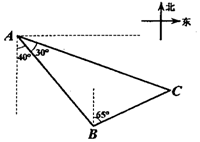 如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.
如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.