题目内容
19．已知向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（ ）| A． | （4，-4） | B． | （6，8） | C． | （5，12） | D． | （3，11） |
分析 由向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），利用向量的坐标运算法则能求出$\overrightarrow{a}$+$\overrightarrow{b}$的坐标．
解答 解：∵向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），
∴$\overrightarrow{a}$+$\overrightarrow{b}$=（6，8）．
故选：B．
点评 本题考查平面向量坐标求法，是基础题，解题时要认真审题，注意向量的坐标运算法则的合理运用．
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
9．在区间[-2，3]上随机取一个数x，则x∈[-1，1]的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{5}$ |
10．
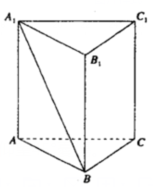如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{14}}{2}$ | D． | $\frac{\sqrt{14}}{4}$ |
7．从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，则甲被选中的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
4．双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是（ ）
| A． | y=$±\frac{5}{4}$x | B． | y=$±\frac{4}{5}$x | C． | y=$±\frac{16}{25}$x | D． | y=±$\frac{25}{16}$x |
11．
一个四棱锥的三视图如图所示，则这个四棱锥的体积等于（ ）
一个四棱锥的三视图如图所示，则这个四棱锥的体积等于（ ）| A． | 8 | B． | 4 | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
8．i是虚数单位，复数$\frac{5i}{1-2i}$等于（ ）
| A． | 2-i | B． | 1-2i | C． | -2+i | D． | -1+2i |