题目内容
15．函数y=cos2x，x∈R的最小正周期为（ ）| A． | 2 | B． | π | C． | 2π | D． | $\frac{1}{π}$ |
分析 由条件利用函数y=Acos（ωx+φ）的周期为$\frac{2π}{ω}$，求得结果．
解答 解：∵y=cos2x，
∴最小正周期T=$\frac{2π}{2}$=π，即函数y=cos2x的最小正周期为π．
故选：B．
点评 本题主要考查函数y=Acos（ωx+φ）的周期性，利用了函数y=Acos（ωx+φ）的周期为$\frac{2π}{ω}$，属于基础题．
练习册系列答案
相关题目
5．f（x）为奇函数，且x＞0时，f（x）=x2-2x，则x＜0时，f（x）=（ ）
| A． | f（x）=x2+2-x | B． | f（x）=x2-2-x | C． | f（x）=-x2+2-x | D． | f（x）=-x2-2-x |
6．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，则z=x+2y的最小值为（ ）
| A． | 0 | B． | 0.5 | C． | 2 | D． | 9 |
3．执行如图的程序框图，若p=4，则输出的S=（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{15}{16}$ | C． | $\frac{31}{32}$ | D． | $\frac{63}{64}$ |
10．
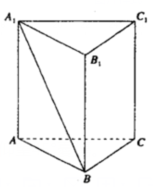如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{14}}{2}$ | D． | $\frac{\sqrt{14}}{4}$ |
20．在等差数列{an}，若a3=16，a9=80，则a6等于（ ）
| A． | 13 | B． | 15 | C． | 17 | D． | 48 |
7．从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，则甲被选中的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
4．双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是（ ）
| A． | y=$±\frac{5}{4}$x | B． | y=$±\frac{4}{5}$x | C． | y=$±\frac{16}{25}$x | D． | y=±$\frac{25}{16}$x |