题目内容
已知函数f(x)=x+
-a
(1)若方程f(x)=0有正根,求实数a的取值范围;
(2)设函数g(x)=|sinx•f(sinx)-sinx|,且g(x)在区间[0,
]上不单调,求实数a的取值范围.
| a |
| x |
(1)若方程f(x)=0有正根,求实数a的取值范围;
(2)设函数g(x)=|sinx•f(sinx)-sinx|,且g(x)在区间[0,
| π |
| 2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)根据方程f(x)=0有正根,转化为方程x2-ax+a=0有正根,对方程进行有异号根,和两正根或一零根一正根进行讨论,即可求得实数a的取值范围.
(2)利用换元法将函数进行转化,根据a的取值情况,结合二次函数的单调性的性质即可得到结论.
(2)利用换元法将函数进行转化,根据a的取值情况,结合二次函数的单调性的性质即可得到结论.
解答:
解:(1)方程f(x)=0有正根?方程x2-ax+a=0有正根.△=a2-4a
①当△=0,即a=0或a=4时,经检验a=4符合题意.
②当△>0,即a>4或a<0时,设方程x2-ax+a=0的两个根为x1、x2,
∵a>4时,使得
成立,
∴a>4符合题意,
∵a<0时,使得x1x2<0成立,
∴a<0符合题意.
综上,a≥4或a<0
(2)设t=sinx,∵x∈[0,
],∴t∈[0,1],
则函数g(x)等价为y=m(t)=|tf(t)-t|在区间[0,1]上不单调.
即m(t)=|t(t+
-a)-t|=|t2-(a+1)t+a|=|(t-1)(t+a)|在区间[0,1]上不单调,
在方程(t-1)(t+a)=0的两个根为t=1或t=-a,
若-a≥1,即a≤-1,此时函数m(t)在(-∞,1]上单调递减,不满足条件.
若-a<1,即a>-1,要使m(t)=|tf(t)-t|在区间[0,1]上不单调,
则对称轴t=-
=
∈(0,1),
即0<
<1,即-1<a<1,
即实数a的取值范围是(-1,1).
①当△=0,即a=0或a=4时,经检验a=4符合题意.
②当△>0,即a>4或a<0时,设方程x2-ax+a=0的两个根为x1、x2,
∵a>4时,使得
|
∴a>4符合题意,
∵a<0时,使得x1x2<0成立,
∴a<0符合题意.
综上,a≥4或a<0
(2)设t=sinx,∵x∈[0,
| π |
| 2 |
则函数g(x)等价为y=m(t)=|tf(t)-t|在区间[0,1]上不单调.
即m(t)=|t(t+
| a |
| t |
在方程(t-1)(t+a)=0的两个根为t=1或t=-a,
若-a≥1,即a≤-1,此时函数m(t)在(-∞,1]上单调递减,不满足条件.
若-a<1,即a>-1,要使m(t)=|tf(t)-t|在区间[0,1]上不单调,
则对称轴t=-
| -(a+1) |
| 2 |
| a+1 |
| 2 |
即0<
| a+1 |
| 2 |
即实数a的取值范围是(-1,1).
点评:本题主要考查函数单调性的应用,利用换元法是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
已知函数f(x)=x2+(m2-4)x+m是偶函数,g(x)=xm在(-∞,0)内单调递增,则实数m=( )
| A、2 | B、±2 | C、0 | D、-2 |
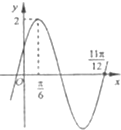 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-
| π |
| 2 |
“m=-2”是“直线mx+2y+2=0与直线2x+my+2=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |