题目内容
若实数a、b、c成等比数列,非零实数x,y分别为a与b,b与c的等差中项,则下列结论正确的是( )
A、
| ||||
B、
| ||||
| C、ax+cy=1 | ||||
| D、ax+cy=2 |
考点:等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:设等比数列a、b、c的公比为q,把b,c用含a与q的代数式表示,由非零实数x,y分别为a与b,b与c的等差中项
把x,y用含a与q的代数式表示,代入
+
整理后得答案.
把x,y用含a与q的代数式表示,代入
| a |
| x |
| c |
| y |
解答:
解:设等比数列a、b、c的公比为q,
则b=aq,c=aq2,
∵非零实数x,y分别为a与b,b与c的等差中项,
∴x=
,y=
,
+
=
+
=
+
=
=2.
故选:B.
则b=aq,c=aq2,
∵非零实数x,y分别为a与b,b与c的等差中项,
∴x=
| a+aq |
| 2 |
| aq+aq2 |
| 2 |
| a |
| x |
| c |
| y |
| a | ||
|
| aq2 | ||
|
| 2 |
| 1+q |
| 2q |
| 1+q |
| 2(1+q) |
| 1+q |
故选:B.
点评:本题考查了等差数列和等比数列的通项公式,考查了学生的计算能力,是基础题.

练习册系列答案
相关题目
已知向量
=(1,-2),
=(-2,1-m),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
函数y=x-
的值域为( )
| 1-x |
| A、(-∞,1) |
| B、(-∞,1] |
| C、(0,1] |
| D、[0,1] |
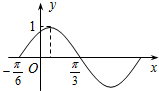 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知{an}是等比数列,对任意n∈N*都有an>0,如果a3(a3+a5)+a4(a4+a6)=25,则a3+a5=( )
| A、5 | B、10 | C、15 | D、20 |