题目内容
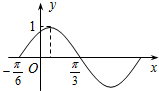函数f（x）=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由图象可得A=1，由周期公式可得ω=2，代入点（
，0）可得φ值，进而可得f（x）=sin（2x+
），再由题意可得x1+x2=
，代入计算可得．
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
解答：
解：由图象可得A=1，
=
-(-
)，解得ω=2，
∴f（x）=sin（2x+φ），
代入点（
，0）可得sin（
+φ）=0
∴
+φ=kπ，∴φ=kπ-
，k∈Z
又|φ|＜
，∴φ=
，
∴f（x）=sin（2x+
），
∴sin（2×
+
）=1，即图中点的坐标为（
，1），
又x1，x2∈(-
，
)，且f（x1）=f（x2）（x1≠x2），
∴x1+x2=
×2=
，
∴f（x1+x2）=sin（2×
+
）=
，
故选：D
| 2π |
| 2ω |
| π |
| 3 |
| π |
| 6 |
∴f（x）=sin（2x+φ），
代入点（
| π |
| 3 |
| 2π |
| 3 |
∴
| 2π |
| 3 |
| 2π |
| 3 |
又|φ|＜
| π |
| 2 |
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
∴sin（2×
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
又x1，x2∈(-
| π |
| 6 |
| π |
| 3 |
∴x1+x2=
| π |
| 12 |
| π |
| 6 |
∴f（x1+x2）=sin（2×
| π |
| 6 |
| π |
| 3 |
| ||
| 2 |
故选：D
点评：本题考查三角函数的图象与解析式，属基础题．
练习册系列答案
相关题目
若实数a、b、c成等比数列，非零实数x，y分别为a与b，b与c的等差中项，则下列结论正确的是（ ）
A、
| ||||
B、
| ||||
| C、ax+cy=1 | ||||
| D、ax+cy=2 |
若集合A={x|x2-7x＜0，x∈N*}，B={y|
∈N*}中元素的个数为（ ）
| 4 |
| y |
| A、3个 | B、2个 | C、1个 | D、0个 |