Question

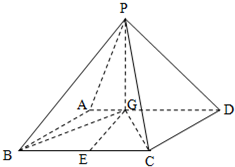如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上且AG=

1

3

GD，BG⊥GC，GB=GC=2，E是BC的中点，四面体P-BCG的体积为

8

3

．
（1）求直线DP到平面PBG所成角的正弦值；
（2）在棱PC上是否存在一点F，使异面直线DF与GC所成的角为60°，若存在，确定点F的位置，若不存在，说明理由．

Answer 1

考点：异面直线及其所成的角,直线与平面所成的角

专题：空间位置关系与距离,空间角

分析：（1）由已知条件推导出PG=4，作DK⊥BG交BG的延长线于K，由已知条件推导出DK⊥面BPG，直线DP与平面PBG所成角为∠DPK，由此能求出直线DP与平面PBG所成角的正弦值．
（3）分别以GB，GC，GP为x，y，z轴建立坐标系，利用向量法能求出满足满足条件的点F不存在．

解答： 解：（1）∵BG⊥GC，GB=GC=2，四面体P-BCG的体积为

8

3

，
∴

1

3

×

1

2

×2×2×PG=

8

3

，解得PG=4，
EG=

1

2

4+4

=

2

，
∵GB=GC=2，AG=

1

3

GD，BG⊥GC，E是BC的中点，
∴△BGC为等腰直角三角形，GE为∠BGC的角平分线，
作DK⊥BG交BG的延长线于K，
∵PG⊥平面ABCD，垂足为G，G在AD上，
∴DK⊥面BPG
∵∠DGK=∠BGA=45°，DK⊥GK，
∴DK=GK，
∵AG=

1

3

GD，
∴DK²=GK²=DG²=（

3

4

AD）²=

9

16

×8=

9

2

，
∴DK=CK=

3

2

．
∵PG=4，DG=

3

4

AD=

3 2

2

，PG⊥DG，
∴PD=

41 2

=

82

2

，
设直线DP与平面PBG所成角为α
∵DK⊥面BPG
∴∠DPK=α，
∴sinα=

DK

DP

=

3 82

82

，
∴直线DP与平面PBG所成角的正弦值为

3 82

82

．…（8分）
（2）∵GB，GC，GP两两垂直，分别以GB，GC，GP为x，y，z轴建立坐标系
假设F存在，
设F（0，y，4-2y）（0＜y＜2），
∵D(-

3

2

，

3

2

，0)，G（0，0，0），C（0，2，0），
∴

DF

=(

3

2

，y-

3

2

，4-2y)，

GC

=(0，2，0)，
又直线DF与GC所成的角为60°
∴cos60°=|

DF

，

GC

|=

|2y-3|

2 9 4 +(y- 3 2 )2+(4-2y)2

=

1

2

，
化简得：y2-7y+

23

2

=0，解得y=

7± 3

2

，不满足0＜y＜2
∴这样的点不存在．…（12分）

点评：本题考查二面角正切值的求法，考查直线与平面所成角的正切值的求法，考查满足条件的点是否存在的判断，综合性强，解题时要注意合理地化空间问题为平面问题，要注意向量法的合理运用．