题目内容
已知函数f(x)=lnx+ax(a∈R)有两个不同的零点x1、x2.
(Ⅰ)求a的取值范围;
(Ⅱ)设x0=
,f′(x)为f(x)的导函数,证明f′(x0)<0;
(Ⅲ)证明:x1x2>e2.
(Ⅰ)求a的取值范围;
(Ⅱ)设x0=
| x1+x2 |
| 2 |
(Ⅲ)证明:x1x2>e2.
考点:导数的运算,函数零点的判定定理
专题:导数的综合应用
分析:(I)f′(x)=
+a(x>0),函数f(x)=lnx+ax(a∈R)有两个不同的零点x1、x2?f′(x)在(0,+∞)有唯一零点.通过对a分类讨论.利用导数研究函数f(x)的单调性即可得出;
(II)不妨设x1<x2.由(I)可知:0<x1<-
<x2.由x>-
时,函数f(x)单调递减,因此只要证明
>-
即可,变为-
-x1>-
.
通过构造函数g(x)=ln(-
-x)+a(-
-x)-(lnx+ax),利用导数研究其单调性即可.
(III)由(II)可得:
>-
.由lnx1+ax1=0,lnx2+ax2=0,可得lnx1+lnx2=-a(x1+x2),再利用基本不等式即可得出.
| 1 |
| x |
(II)不妨设x1<x2.由(I)可知:0<x1<-
| 1 |
| a |
| 1 |
| a |
| x1+x2 |
| 2 |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
通过构造函数g(x)=ln(-
| 2 |
| a |
| 2 |
| a |
(III)由(II)可得:
| x1+x2 |
| 2 |
| 1 |
| a |
解答:
解:(I)f′(x)=
+a(x>0),当a≥0时,f′(x)>0,函数f(x)单调递增,此时函数f(x)最多有一个零点,不符合题意,应舍去;
当a<0时,令f′(x)=0,解得x=-
.当0<x<-
时,f′(x)>0,此时函数f(x)单调递增;当x>-
时,f′(x)<0,此时函数f(x)单调递减法.
可知-
是函数f(x)的极大值点即最大值点,且当x→0时,f(x)→-∞;当x→+∞时,f(x)→-∞.
又函数f(x)=lnx+ax(a∈R)有两个不同的零点x1、x2.∴f(x)max>0,即ln(-
)-1>0,解得-
<a<0.
∴a的取值范围是(-
,0).
(II)不妨设x1<x2.
由(I)可知:0<x1<-
<x2.
∵x>-
时,函数f(x)单调递减,∴只要证明
>-
即可,变为-
-x1>-
.
设g(x)=ln(-
-x)+a(-
-x)-(lnx+ax),
∴g′(x)=
-2a-
=
<0,x∈(0,-
),且g(
)=0.
∴g(-
-x1)<g(-
).
∴-
-x1>-
.
(III)由(II)可得:
>-
.
∵lnx1+ax1=0,lnx2+ax2=0,
∴lnx1+lnx2=-a(x1+x2)>-a×(-
)=2,
∴x1x2>e2.
| 1 |
| x |
当a<0时,令f′(x)=0,解得x=-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
可知-
| 1 |
| a |
又函数f(x)=lnx+ax(a∈R)有两个不同的零点x1、x2.∴f(x)max>0,即ln(-
| 1 |
| a |
| 1 |
| e |
∴a的取值范围是(-
| 1 |
| e |
(II)不妨设x1<x2.
由(I)可知:0<x1<-
| 1 |
| a |
∵x>-
| 1 |
| a |
| x1+x2 |
| 2 |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
设g(x)=ln(-
| 2 |
| a |
| 2 |
| a |
∴g′(x)=
| 1 | ||
|
| 1 |
| x |
| -2(ax+1)2 |
| x(2+ax) |
| 2 |
| a |
| -1 |
| a |
∴g(-
| 2 |
| a |
| 1 |
| a |
∴-
| 2 |
| a |
| 1 |
| a |
(III)由(II)可得:
| x1+x2 |
| 2 |
| 1 |
| a |
∵lnx1+ax1=0,lnx2+ax2=0,
∴lnx1+lnx2=-a(x1+x2)>-a×(-
| 2 |
| a |
∴x1x2>e2.
点评:本题考查了利用导数研究函数单调性极值与最值,考查了构造函数解决问题的方法,考查了分类讨论的思想方法,考查了推理能力化为计算能力,属于难题.

练习册系列答案
相关题目
为得到函数y=cos(2x+3)的图象,只需将函数y=cos2x的图象( )
| A、向左平移3个长度单位 | ||
| B、向右平移3个长度单位 | ||
C、向左平移
| ||
D、向右平移
|
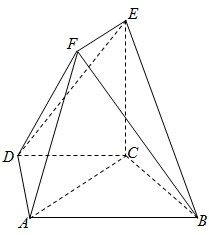 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=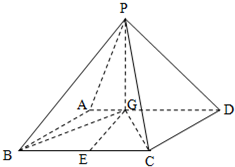 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=