题目内容
如图1,在平行四边形ABCD中,∠A=90°,∠B=135°,∠C=60°,AB=AD,M,N分别是边AB,CD上的点,且2AM=MD,2CN=ND,如图1,将△ABD沿对角线BD折叠,使得平面ABD⊥平面BCD,并连结AC,MN(如图2).
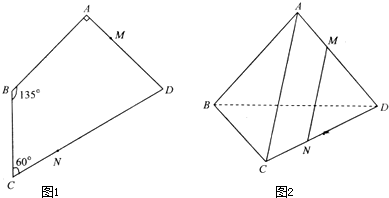
(1)证明:MN∥平面ABC;
(2)证明:AD⊥BC;
(3)若BC=1,求三棱锥A-BCD的体积.

(1)证明:MN∥平面ABC;
(2)证明:AD⊥BC;
(3)若BC=1,求三棱锥A-BCD的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)先证明出MN∥AC,继而根据线面平行的判定定理证明出MN∥平面ABC.
(2)先证明出BC⊥BD,根据线面垂直的判定定理证明出BC⊥平面ABD,最后由线面垂直的性质可推断出AD⊥BC.
(3)分别在△BCD和△ABD中求得BD和AB,则三角形ABD的面积可得,最后利用VA-BCD=VC-ABD求得三棱锥的体积.
(2)先证明出BC⊥BD,根据线面垂直的判定定理证明出BC⊥平面ABD,最后由线面垂直的性质可推断出AD⊥BC.
(3)分别在△BCD和△ABD中求得BD和AB,则三角形ABD的面积可得,最后利用VA-BCD=VC-ABD求得三棱锥的体积.
解答:
(1)证明:在△ACD中,
∵2AM=MD,2NC=ND,
∴MN∥AC,
∵MN?平面ABC,AC?平面ABC,
∴MN∥平面ABC.
(2)证明:在△ABD中,AB=AD,∠A=90°,
∴∠ABD=45°,
∵在平面四边形ABCD中,∠B=135°,
∴BC⊥BD,
∵平面ABD⊥平面BCD,BC?平面BCD,平面ABD∩平面BCD=BD,
∴BC⊥平面ABD,
又AD?平面ABD,
∴AD⊥BC.
(3)解:在△BCD中,
∵BC=1,∠CBD=90°,∠BCD=60°,
∴BD=
,
在△ABD中,∠A=90°,AB=AD,
∴AB=
,
∴S△ABD=
AB•AD=
,
由(2)知BC⊥平面ABD,
∴VA-BCD=VC-ABD=
×
×1=
.
∵2AM=MD,2NC=ND,
∴MN∥AC,
∵MN?平面ABC,AC?平面ABC,
∴MN∥平面ABC.
(2)证明:在△ABD中,AB=AD,∠A=90°,
∴∠ABD=45°,
∵在平面四边形ABCD中,∠B=135°,
∴BC⊥BD,
∵平面ABD⊥平面BCD,BC?平面BCD,平面ABD∩平面BCD=BD,
∴BC⊥平面ABD,
又AD?平面ABD,
∴AD⊥BC.
(3)解:在△BCD中,
∵BC=1,∠CBD=90°,∠BCD=60°,
∴BD=
| 3 |
在△ABD中,∠A=90°,AB=AD,
∴AB=
| ||
| 2 |
∴S△ABD=
| 1 |
| 2 |
| 3 |
| 4 |
由(2)知BC⊥平面ABD,
∴VA-BCD=VC-ABD=
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查空间点、线、面的位置关系及三棱锥的体积.考查空间想象能力、运算能力和逻辑推理能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
在复平面内,复数-2+3i对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
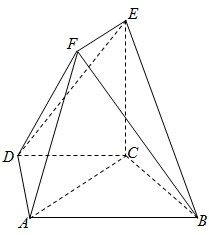 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=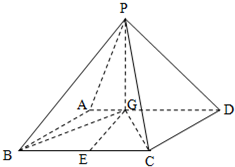 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=