题目内容
已知点A(1,1),B(2,-1).
(Ⅰ)求直线AB的方程,并判断直线AB的倾斜角是锐角还是钝角;
(Ⅱ)若点P在x轴上,且∠ABP=90°,求△ABP的面积.
(Ⅰ)求直线AB的方程,并判断直线AB的倾斜角是锐角还是钝角;
(Ⅱ)若点P在x轴上,且∠ABP=90°,求△ABP的面积.
考点:直线的一般式方程与直线的垂直关系,直线的倾斜角
专题:直线与圆
分析:(Ⅰ)先求出直线AB的kAB,再求直线AB的方程,由kAB=-2<0,得到直线AB的倾斜角为钝角.
(Ⅱ)设点P的坐标为P(x,0),由∠ABP=90°,得点P的坐标P(4,0).由此能求出△ABP的面积.
(Ⅱ)设点P的坐标为P(x,0),由∠ABP=90°,得点P的坐标P(4,0).由此能求出△ABP的面积.
解答:
解:(Ⅰ)∵A(1,1),B(2,-1),
∴kAP=
=-2,
∴直线AB的方程为;y-1=-2(x-1),
整理,得2x+y-3=0,
∵kAB=-2<0,
∴直线AB的倾斜角为钝角.
(Ⅱ)设点P的坐标为P(x,0),
∵∠ABP=90°,∴AB⊥BP,
∴kAB•kPB=-1,∴
•(-2)=-1,
解得x=4,∴点P的坐标P(4,0).
∵|AB|=
=
,
点P(4,0)到直线AB:2x+y-3=0的距离
d=
=
,
∴△ABP的面积S△ABP=
×
×
=
.
∴kAP=
| 1-(-1) |
| 1-2 |
∴直线AB的方程为;y-1=-2(x-1),
整理,得2x+y-3=0,
∵kAB=-2<0,
∴直线AB的倾斜角为钝角.
(Ⅱ)设点P的坐标为P(x,0),
∵∠ABP=90°,∴AB⊥BP,
∴kAB•kPB=-1,∴
| 1 |
| x-2 |
解得x=4,∴点P的坐标P(4,0).
∵|AB|=
| (2-1)2+(-1-1)2 |
| 5 |
点P(4,0)到直线AB:2x+y-3=0的距离
d=
| |8+0-3| | ||
|
| 5 |
∴△ABP的面积S△ABP=
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题考查直线方程的求法,考查三角形面积的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知离散型随机变量ξ的分布列如下表所示:
则表中p值等于( )
| ξ | 0 | 1 | 2 |
| P | 0.4 | p | 0.3 |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
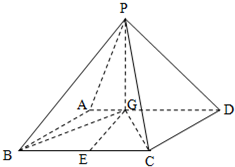 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=