题目内容
直线
+
=1与两坐标轴围成的三角形的周长为（ ）
| x |
| 3 |
| y |
| 4 |
| A、6 | B、7 | C、12 | D、14 |
考点：直线的截距式方程
专题：直线与圆
分析：由截距式方程可得直线过A（3，0），B（0，4），易得三角形的周长．
解答：
解：由直线方程
+
=1可知直线过点A（3，0），B（0，4），
∴由勾股定理可得AB=
=5，
∴所围成的三角形的周长为3+4+5=12
故选：C．
| x |
| 3 |
| y |
| 4 |
∴由勾股定理可得AB=
| 32+42 |
∴所围成的三角形的周长为3+4+5=12
故选：C．
点评：本题考查直线的截距式方程，属基础题．
练习册系列答案
相关题目
在△ABC中，已知∠C=60°．a，b，c分别为∠A，∠B，∠C的对边，则
+
为（ ）
| a |
| b+c |
| b |
| c+a |
A、3-2
| ||
| B、1 | ||
C、3-2
| ||
D、3+2
|
曲线f（x）=x2+x+1在点（0，1）处的切线方程为（ ）
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
在复平面内，复数-2+3i对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知离散型随机变量ξ的分布列如下表所示：
则表中p值等于（ ）
| ξ | 0 | 1 | 2 |
| P | 0.4 | p | 0.3 |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
为得到函数y=cos（2x+3）的图象，只需将函数y=cos2x的图象（ ）
| A、向左平移3个长度单位 | ||
| B、向右平移3个长度单位 | ||
C、向左平移
| ||
D、向右平移
|
在两个袋内，分别装着写有0，1，2，3，4，5六个数字的6张卡片，今从每个袋中各任取一张卡片，则两数之和等于5的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
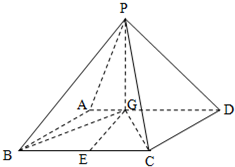如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上且AG=